
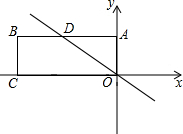
 如图,在平面直角坐标系中,矩形OABC的顶点A在y轴正半轴上,边AB、OA(AB>OA)的长分别是方程x2-11x+24=0的两个根,D是AB上的点,且满足$\frac{DA}{DB}=\frac{3}{5}$.
如图,在平面直角坐标系中,矩形OABC的顶点A在y轴正半轴上,边AB、OA(AB>OA)的长分别是方程x2-11x+24=0的两个根,D是AB上的点,且满足$\frac{DA}{DB}=\frac{3}{5}$.分析 (1)根据边AB、OA(AB>OA)的长分别是方程x2-11x+24=0的两个根,即可得到AO=3,AB=8,进而得出矩形OABC的面积以及矩形OABC的周长;
(2)根据$\frac{DA}{DB}=\frac{3}{5}$,AB=8,可得AD=3,再根据AO=3,进而得出D(-3,3),再根据待定系数法即可求得直线OD的解析式;
(3)根据△PAD是等腰三角形,分4种情况讨论:当AD=AP1=3时,当DA=DP2=3时,当AP3=DP3时,当DA=DP4=3时,分别根据等腰直角三角形的性质,求得点P的坐标.
解答  解:(1)∵x2-11x+24=0,
解:(1)∵x2-11x+24=0,
∴(x-3)(x-8)=0,
∴x1=3,x2=8,
∵AB、OA(AB>OA)的长分别是方程x2-11x+24=0的两个根,
∴AO=3,AB=8,
∴矩形OABC的面积=3×8=24,矩形OABC的周长=2(3+8)=22,
故答案为:24,22;
(2)∵$\frac{DA}{DB}=\frac{3}{5}$,AB=8,
∴AD=3,
又∵AO=3,
∴D(-3,3),
设直线OD解析式为y=kx,则
3=-3k,即k=-1,
∴直线OD的解析式为y=-x;
(3)∵AD=AO=3,∠DAO=90°,
∴△AOD是等腰直角三角形,
∴∠ADO=45°,DO=3$\sqrt{2}$,
根据△PAD是等腰三角形,分4种情况讨论: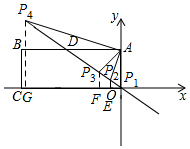
①如图所示,当AD=AP1=3时,点P1的坐标为(0,0);
②如图所示,当DA=DP2=3时,过P2作x轴的垂线,垂足为E,则
OP2=3$\sqrt{2}$-3,△OEP2是等腰直角三角形,
∴P2E=OE=$\frac{3\sqrt{2}-3}{\sqrt{2}}$=3-$\frac{3}{2}\sqrt{2}$,
∴点P2的坐标为(-3+$\frac{3}{2}\sqrt{2}$,3-$\frac{3}{2}\sqrt{2}$);
③如图所示,当AP3=DP3时,∠DAP3=∠ADO=45°,
∴△ADP3是等腰直角三角形,
∴DP3=$\frac{AD}{\sqrt{2}}$=$\frac{3}{2}\sqrt{2}$,
∴P3O=3$\sqrt{2}$-$\frac{3}{2}\sqrt{2}$=$\frac{3}{2}\sqrt{2}$,
过P3作x轴的垂线,垂足为F,则△OP3F是等腰直角三角形,
∴P3F=OF=$\frac{3}{2}$,
∴点P3的坐标为(-$\frac{3}{2}$,$\frac{3}{2}$);
④如图所示,当DA=DP4=3时,P4O=3+3$\sqrt{2}$,
过P4作x轴的垂线,垂足为G,则△OP4G是等腰直角三角形,
∴P4G=OG=$\frac{3}{2}\sqrt{2}$+3,
∴点P4的坐标为(-3-$\frac{3}{2}$$\sqrt{2}$,3+$\frac{3}{2}$$\sqrt{2}$);
综上所述,当△PAD是等腰三角形时,点P的坐标为(0,0)、(-3+$\frac{3}{2}\sqrt{2}$,3-$\frac{3}{2}\sqrt{2}$)、(-$\frac{3}{2}$,$\frac{3}{2}$)、(-3-$\frac{3}{2}$$\sqrt{2}$,3+$\frac{3}{2}$$\sqrt{2}$).
点评 本题属于相似形综合题,主要考查了等腰直角三角形的性质,矩形的性质,等腰三角形的判定,解一元二次方程以及待定系数法求一次函数解析式的综合应用,解题时注意:当△PAD是等腰三角形时,需要分情况讨论,解题时注意分类思想的运用.解决问题的关键是作辅助线构造等腰直角三角形.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图在3×3的正方形网格中,现在已有4个小方格已涂上阴影,其余5个小方格是空白的,除此以外小方格完全相同.
如图在3×3的正方形网格中,现在已有4个小方格已涂上阴影,其余5个小方格是空白的,除此以外小方格完全相同.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用如图所示的两个转盘进行“配紫色”游戏,每个转盘都被分成面积相等的三个扇形,游戏者同时转动两个转盘,请用树状图或列表说明配成紫色的概率是多少(蓝色和红色能配成紫色)?
用如图所示的两个转盘进行“配紫色”游戏,每个转盘都被分成面积相等的三个扇形,游戏者同时转动两个转盘,请用树状图或列表说明配成紫色的概率是多少(蓝色和红色能配成紫色)?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com