
【题目】已知a与b满足![]() ,数轴上点A 和点B 所对应的数分别为a和b,点P 为数轴上一动点,其对应的数为
,数轴上点A 和点B 所对应的数分别为a和b,点P 为数轴上一动点,其对应的数为![]() .
.
(1)求a,b的值.
(2)若点 P 到点 A、点 B 的距离相等,求点P对应的数.
(3)现在点 A、点 B 分别以 2 个单位长度/秒和 0.5 个单位长度/秒的速度同时向右运动,点 P 以 3 个单位长度/秒的速度同时从原点向左运动.当点 A 与点 B 之间的距离为2个单位长度时,求点 P 所对应的数是多少?
![]()
【答案】(1)![]() -1,
-1, ![]() 3;(2)P表示1;(3)P表示-4或-12.
3;(2)P表示1;(3)P表示-4或-12.
【解析】
(1)根据绝对值的性质以及偶次方的意义得出a,b的值;(2)利用点P到点A,点B的距离相等,A为-1,B为3,即可得出P的位置;(3)分两种情况讨论:①当点A在点B左边两点相距2个单位时;②当点A在点B右边时,两点相距2个单位时;分别求出t的值,然后求出点P对应的数即可.
解:(1)∵![]() ,
,
∴a+1=0,b-3=0,
∴a=-1,b=3;
(2)∵点P到点A,点B的距离相等,A为-1,B为3,
∴x=![]() =1;
=1;
∴点P对应的数为1.
(3)①当点A在点B左边,两点相距2个单位时,此时需要的时间为t,
则3+0.5t-(-1+2t)=2,
解得:t=![]() ,
,
则点P对应的数为-3![]() =-4;
=-4;
②当点A在点B右边,两点相距2个单位时,此时需要的时间为t,
则-1+2t -(3+0.5t)=2,
解得:t=4,
则点P对应的数为-3×4=-12;
综上可得,当点A与点B之间的距离为2个单位长度时,求点P所对应的数是-4或-12.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
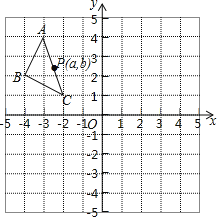
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,4),B(-4,2),C(-2,1),且△A1B1C1与△ABC关于原点O成中心对称。
(1)画出△A1B1C1,并写出点A1的坐标;
(2)P(a,b)是△ABC的AC边上一点,△ABC经平移后点P的对应点为P'(a+3,b+1),请画出平移后的△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2 h,并且甲车途中休息了0.5 h,如图是甲、乙两车行驶的路程y(km)与时间x(h)的函数图象.
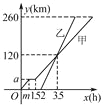
(1)求出图中m和a的值.
(2)求出甲车行驶的路程y(km)与时间x(h)的函数关系式,并写出相应的x的取值范围.
(3)当乙车行驶多长时间时,两车恰好相距50 km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义函数:在y关于x的函数中,若0≤x≤1时,函数y有最大值和最小值,分别记ymax和ymin , 且满足 ![]() ,则我们称函数y为“三角形函数”.
,则我们称函数y为“三角形函数”.
(1)若函数y=x+a为“三角形函数”,求a的取值范围;
(2)判断函数y=x2﹣ ![]() x+1是否为“三角形函数”,并说明理由;
x+1是否为“三角形函数”,并说明理由;
(3)已知函数y=x2﹣2mx+1,若对于0≤x≤1上的任意三个实数a,b,c所对应的三个函数值都能构成一个三角形的三边长,则求满足条件的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1…过点A1作y轴的垂线交L2于点A2,过点A2作x轴的垂线交于点A3,过点A3作y轴的垂线交L2于点A4,依次进行下去,则点A2018的坐标为( )
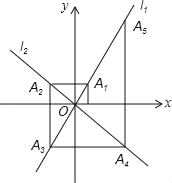
A. (﹣21009,21009) B. (﹣21009,﹣21010)
C. (﹣1009,1009) D. (﹣1009,﹣2018)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,直线y=﹣![]() x+4交坐标轴于A、B两点,过点C(﹣4,0)作CD⊥AB于D,交y轴于点E.
x+4交坐标轴于A、B两点,过点C(﹣4,0)作CD⊥AB于D,交y轴于点E.
(1)求证:△COE≌△BOA;
(2)如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.
①判断△OMN的形状.并证明;
②当△OCM和△OAN面积相等时,求点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
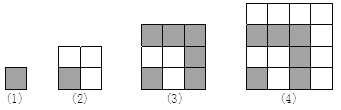
【题目】用同样大小的两种不同颜色的正方形纸片,按下图方式拼正方形.
 …
…
第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形有1+3+5=9个小正方形;
第(4)个图形有25小正方形;
……
(1)根据上面的发现我们可以猜想:1+3+5+7+…+(2n-1)的结果(用含n的代数式表示);
(2)请根据你的发现计算:① 1+3+5+7+…+99;
② 101+103+105+…+199.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com