
【题目】如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积 . 
【答案】![]()
【解析】解:由题意点B′在射线BA上,D′在过D垂直PF的直线上,
易知当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的图形是图中平行四边形AD′D″B″.
作D′M⊥AB于M,DN⊥AB于N,
在等腰梯形ABDD′中,易知四边形MNDD′是矩形,BN=AM= ![]() ,MN=DD′=5﹣
,MN=DD′=5﹣ ![]() =
= ![]() ,DN=
,DN= ![]() ,
,
∵BD=DC,DD″∥AB,
∴AD″=D″C,
在Rt△ADC中,DD″= ![]() AC=
AC= ![]() ,
,
∴D′D″=DD″﹣DD′= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积= ![]() ×
× ![]() =
= ![]() ,
,
所以答案是 ![]() .
.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设![]() ,
,![]() ,满足
,满足![]() .
.
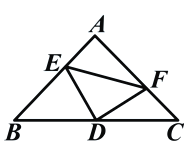
(1)求BE及CF的长。
(2)求证:![]() 。
。
(3)在(1)的条件下,求△DEF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a与b满足![]() ,数轴上点A 和点B 所对应的数分别为a和b,点P 为数轴上一动点,其对应的数为
,数轴上点A 和点B 所对应的数分别为a和b,点P 为数轴上一动点,其对应的数为![]() .
.
(1)求a,b的值.
(2)若点 P 到点 A、点 B 的距离相等,求点P对应的数.
(3)现在点 A、点 B 分别以 2 个单位长度/秒和 0.5 个单位长度/秒的速度同时向右运动,点 P 以 3 个单位长度/秒的速度同时从原点向左运动.当点 A 与点 B 之间的距离为2个单位长度时,求点 P 所对应的数是多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:一个矩形的两邻边之比为 ![]() ,则称该矩形为“特比矩形”.
,则称该矩形为“特比矩形”.
(1)如图①,在“特比矩形”ABCD中, ![]() =
= ![]() ,求∠AOD的度数;
,求∠AOD的度数; 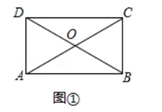
(2)如图②,特比矩形CDEF的边CD在半圆O的直径AB上,顶点E、F在半圆上,已知直径AB= ![]() ,求矩形CDEF的面积;
,求矩形CDEF的面积; 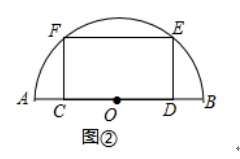
(3)在平面直角坐标系xOy中,⊙O的半径为 ![]() ,点Q的坐标为(q,2
,点Q的坐标为(q,2 ![]() ),如果在⊙O上存在一点P,过点P作x轴的垂线与过点Q作y轴的垂线交于点M,过点P作y轴的垂线与过点Q作x轴的垂线交于点N,以点P、Q、M、N为顶点的矩形是“特比矩形”,请直接写出q的取值范围.
),如果在⊙O上存在一点P,过点P作x轴的垂线与过点Q作y轴的垂线交于点M,过点P作y轴的垂线与过点Q作x轴的垂线交于点N,以点P、Q、M、N为顶点的矩形是“特比矩形”,请直接写出q的取值范围. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com