
已知抛物线y= x2+bx+c过点(-6,-2),与y轴交于点C,且对称轴与x轴交于点B(-2,0),顶点为A.
x2+bx+c过点(-6,-2),与y轴交于点C,且对称轴与x轴交于点B(-2,0),顶点为A.
(1)求该抛物线的解析式和A点坐标;
(2)若点D是该抛物线上的一个动点,且使△DBC是以B为直角顶点BC为腰的等腰直角三角形,求点D坐标;
(3)若点M是第二象限内该抛物线上的一个动点,经过点M的直线MN与y轴交于点N,是否存在以O、M、N为顶点的三角形与△OMB全等?若存在,请求出直线MN的解析式;若不存在,请说明理由.

(1)A点的坐标为(﹣2,6);
(2)D点的坐标为:(2,﹣2);
(3)存在.直线MN的解析式为y=6或y=﹣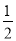 x+2.
x+2.
【解析】
试题分析:(1)首先依据顶点坐标先求出b的值,然后利用待定系数法求出抛物线的解析式;
(2)过B点作CB的垂线交抛物线与D,然后过D点作x轴的垂线,垂足为E,通过三角形全等即可求得点D的坐标.
(3)由于三角形的各边,只有OB=2是确定长度的,因此可以以OB为基准进行分类讨论:
①OB=OM.因为第二象限内点P到原点的距离均大于4,因此OB≠OM,此种情形排除;
②OB=ON.分析可知,只有如答图2所示的情形成立;
③OB=MN.分析可知,只有如答图3所示的情形成立.
试题解析:(1)∵对称轴与x轴交于点B(﹣2,0),
∴A的横坐标为:x=﹣2,
∴﹣ =﹣2,
=﹣2,
解得;b=﹣2,
∴抛物线为y=﹣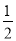 x2﹣2x+c,
x2﹣2x+c,
∵抛物线y=﹣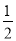 x2+bx+c过点(﹣6,﹣2),
x2+bx+c过点(﹣6,﹣2),
∴代入得﹣2=﹣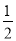 ×(﹣6)2﹣2×(﹣6)+c,解得c=4,
×(﹣6)2﹣2×(﹣6)+c,解得c=4,
∴该抛物线的解析式为:y=﹣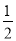 x2﹣2x+4,
x2﹣2x+4,
∴y=﹣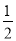 x2﹣2x+4=﹣
x2﹣2x+4=﹣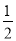 (x2+4x+4)+6)=﹣
(x2+4x+4)+6)=﹣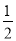 (x+2)2+6
(x+2)2+6
∴A点的坐标为(﹣2,6);
(2)过B点作CB的垂线交抛物线与D,然后过D点作x轴的垂线,垂足为E,
∵∠CBD=90°,
∴∠CBO+∠EBD=90°,
∵∠BCO+∠CBO+90°,
∴∠EBD=∠BCO,∠CBO=∠BDE,
∴在△CBO与△BDE中

∴△CBO≌△BDE(ASA)
∴DE=OB=2,BE=OC=4
∴D点的坐标为(2,﹣2)或(﹣6.2),
把(2,﹣2)或(﹣6.2)分别代入y=﹣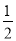 x2﹣2x+4,(﹣2,2)合适,(﹣6,2)不合适,
x2﹣2x+4,(﹣2,2)合适,(﹣6,2)不合适,
∴D点的坐标为:(2,﹣2)
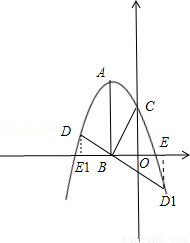
图1
(3)存在.
若以O、M、N为顶点的三角形与△OBM全等,可能有以下情形:
(I)OB=OM.
由图象可知,OM最小值为4,即OM≠OB,故此种情形不存在.
(II)OB=ON.
若点M在y轴正半轴上,如答图2所示:
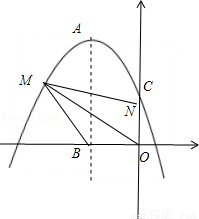
图2
此时△OBM≌△OMN,
∴∠OMB=∠OMN,即点P在第二象限的角平分线上,ON=OB=2,M点坐标为:(4,4),
∴直线PE的解析式为:y=﹣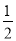 x+2;
x+2;
若点E在y轴负半轴上,易知此种情形下,两个三角形不可能全等,故不存在.
(III)OB=MN.
∵OB=2,
∴第二象限内对称轴左侧的点到y轴的距离均大于2,
则点M只能位于对称轴右侧或与顶点A重合.
若点M位于第二象限内抛物线对称轴的右侧,易知△OMN为钝角三角形,而△OMB为锐角三角形,则不可能全等;
若点M与点A重合,如答图3所示,此时△OBM≌△OMN,四边形MNOB为矩形,

图3
∴直线MN的解析式为:y=6.
综上所述,存在以O、M、N为顶点的三角形与△OMB全等,直线MN的解析式为y=6,y=﹣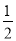 x+2.
x+2.
考点:二次函数综合题.


科目:初中数学 来源:2013-2014学年江苏省南京市六合区中考一模数学试卷(解析版) 题型:选择题
a满足以下说法:①a是无理数;②2<a<3;③a2是整数.那么a可能是( )
A. B.
B.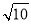 C.2.5 D.
C.2.5 D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(即一模)数学试卷(解析版) 题型:填空题
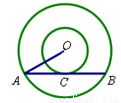
如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于C点,sinA= ,OA=10cm,则AB长为 cm.
,OA=10cm,则AB长为 cm.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(即一模)数学试卷(解析版) 题型:选择题
下列说法正确的是( )
A.某种彩票的中奖机会是1%,则买100张这种彩票一定会中奖.
B.为了解全国中学生的睡眠情况,应该采用普查的方式.
C.一组数据3,5,4,5,5,6,10的众数和中位数都是5.
D.若甲数据的方差s甲2=0.05,乙数据的方差s乙2=0.1,则乙数据比甲数据稳定.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(二模)数学试卷(解析版) 题型:解答题
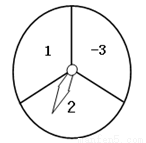
如图所示的转盘,分成三个相同的扇形,3个扇形分别标有数字1、2、-3,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,重新转动转盘).
(1)写出此情景下一个不可能发生的事件;
(2)用树状图或列表法,求事件“转动两次,第一次得到的数与第二次得到的数和为正数”发生的概率.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(二模)数学试卷(解析版) 题型:填空题
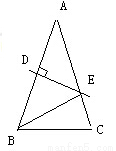
如图,在△ABC中,AB=AC, ∠A=40º,AB的垂直平分线交AC于点E,垂足为点D,连接BE,则∠EBC的度数为 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏大丰刘庄第二初中九年级下学期第一次月考数学试卷(解析版) 题型:解答题
2013年3月1日,张老师就本班学生对心理健康知识的了解程度进行了一次调查统计,下图是他采集数据后绘制的两幅不完整的统计图(A:不了解,B:一般了解,C:了解较多,D:熟悉).请你根据图中提供的信息解答以下问题:


(1)求该班共有多少名学生;
(2)在条形统计图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏仪征大仪中学九年级3月月考数学试卷(解析版) 题型:填空题
今年3月底在上海和安徽两地发现的H7N9型禽流感是一种新型禽流感.研究表明,禽流感病毒的颗粒呈球形,杆状或长丝状,其最小直径约为80nm,1nm=0.000000001m,其最小直径用科学计数法表示约为___m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com