
分析 分两种情况:
解法一:①当E在BA的延长线上时,如图1,作辅助线,构建直角三角形,先根据勾股定理列等式求AH的长,从而继续求CH、BH的长,从而可以求EC的长,设FN=a,则EN=2a,可求FN=$\frac{2\sqrt{5}}{5}$,EN=$\frac{4\sqrt{5}}{5}$,由此求EF的长,得出AF的长;
②当E在线段AB上时,如图2,同样的方法可求得AF的长.
解法二,两种情况都设某一个角为x°,分别表示其它角,利用等角对等边,得出线段的长,计算AF的长.
解答 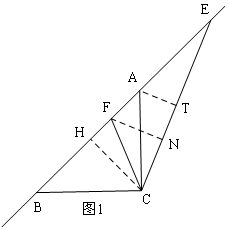 解法一:分两种情况:
解法一:分两种情况:
①当E在BA的延长线上时,如图1,
过C作CH⊥AB于H,
设AH=x,则BH=2.5-x,
由勾股定理得:CH2=AC2-AH2=1.52-x2,
CH2=BC2-BH2=22-(2.5-x)2,
∴1.52-x2=22-(2.5-x)2,
x=0.9,
∴AH=0.9,
∴HE=AH+AE=0.9+1.5=2.4,
CH=$\sqrt{A{C}^{2}-A{H}^{2}}$=$\sqrt{1.{5}^{2}-0.{9}^{2}}$=1.2,
在Rt△ECH中,EC=$\sqrt{C{H}^{2}+H{E}^{2}}$=$\sqrt{1.{2}^{2}+2.{4}^{2}}$=$\frac{6\sqrt{5}}{5}$,
过F作FN⊥EC于N,过A作AT⊥EC于T,
由tan∠E=$\frac{CH}{EH}=\frac{FN}{EN}=\frac{1.2}{2.4}=\frac{1}{2}$,
设FN=a,则EN=2a,
∵∠ECF=45°,
∴△FCN是等腰直角三角形,
∴FN=NC=a,
∴EC=EN+CN=2a+a=$\frac{6\sqrt{5}}{5}$,
a=$\frac{2\sqrt{5}}{5}$,
在△EFN中,FN=$\frac{2\sqrt{5}}{5}$,EN=$\frac{4\sqrt{5}}{5}$,
∴EF=$\sqrt{F{N}^{2}+E{N}^{2}}$=2,
∴AF=EF-AE=2-1.5=0.5;
②当E在线段AB上时,如图2,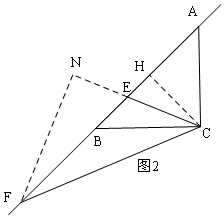
过C作CH⊥AB于H,
同理得:AH=0.9,CH=1.2,
∵AC=AE=1.5,
∴EH=AE-AH=1.5-0.9=0.6,
由勾股定理得:CE=$\sqrt{1.{2}^{2}-0.{6}^{2}}$=$\frac{3\sqrt{5}}{5}$,
∴tan∠ECH=$\frac{EH}{CH}=\frac{1}{2}$,
过F作FN⊥EC于N,
∵∠ECF=45°,
∴△FCN是等腰直角三角形,
∴FN=CN,
∵∠FNC=∠EHC=90°,
∠NEF=∠HEC,
∴∠NFE=∠ECH,
∴tan∠NFE=$\frac{EN}{FN}=\frac{1}{2}$,
∴FN=CN=2EN,
∴CE=EN=$\frac{3\sqrt{5}}{5}$,
由勾股定理得:EF=$\sqrt{F{N}^{2}+E{N}^{2}}$=$\sqrt{(\frac{6\sqrt{5}}{5})^{2}+(\frac{3\sqrt{5}}{5})^{2}}$=3,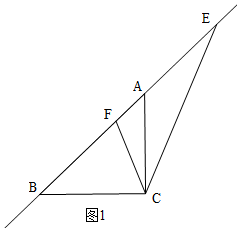
∴AF=AE+EF=1.5+3=4.5,
综上所述,AF的长为0.5或4.5;
解法二:分两种情况:
①当E在BA的延长线上时,如右图1,
设∠E=x°,则∠ACE=x°,∠ACF=45°-x°,
∵∠ACB=90°,
∴∠BCF=90°-(45°-x°)=45°+x°,
∵∠CFB=∠E+∠ECF=45°+x°,
∴∠BCF=∠CFB,
∴BC=BF=2,
∴AF=AB-BF=2.5-2=0.5;
②当E在线段AB上时,如右图2,
设∠AEC=x°,则∠ACE=x°,
∴∠BCE=90°-x°,
∴∠BCF=∠ECF-∠BCE=45°-(90°-x°)=x°-45°,
∵∠F=x°-45°,
∴∠F=∠BCF,
∴BC=BF=2,
∴AF=AB+BF=2.5+2=4.5,
故答案为:0.5或4.5.
点评 本题考查了勾股定理、等腰直角三角形的性质和判定、同角的三角函数,熟练掌握勾股定理列方程是关键,恰当地作辅助线是本题的突破口,有难度,同时要注意“E、F均在直线AB上”,根据数形结合采用分类讨论的思想解决问题.


科目:初中数学 来源: 题型:解答题
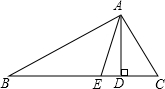 如图,在△ABC中,∠B=30°,∠C=50°,AE是∠BAC的平分线,AD是高.
如图,在△ABC中,∠B=30°,∠C=50°,AE是∠BAC的平分线,AD是高.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com