
【题目】为进一步建设秀美、宜居的生态环境,某村欲购买甲、乙、丙三种树美化村庄,已知甲、乙丙三种树的价格之比为2:2:3,甲种树每棵200元,现计划用210000元资金,购买这三种树共1000棵.
(1)求乙、丙两种树每棵各多少元?
(2)若购买甲种树的棵树是乙种树的2倍,恰好用完计划资金,求这三种树各能购买多少棵?
(3)若又增加了10120元的购树款,在购买总棵树不变的前提下,求丙种树最多可以购买多少棵?
【答案】
(1)解:已知甲、乙丙三种树的价格之比为2:2:3,甲种树每棵200元,
则乙种树每棵200元,
丙种树每棵 ![]() ×200=300(元)
×200=300(元)
(2)解:设购买乙种树x棵,则购买甲种树2x棵,丙种树(1000﹣3x)棵.
根据题意:
200×2x+200x+300(1000﹣3x)=210000,
解得x=300
∴2x=600,1000﹣3x=100,
答:能购买甲种树600棵,乙种树300棵,丙种树100棵
(3)解:设购买丙种树y棵,则甲、乙两种树共(1000﹣y)棵,
根据题意得:
200(1000﹣y)+300y≤210000+10120,
解得:y≤201.2,
∵y为正整数,
∴y最大取201.
答:丙种树最多可以购买201棵
【解析】(1)利用已知甲、乙丙三种树的价格之比为2:2:3,甲种树每棵200元,即可求出乙、丙两种树每棵钱数;(2)假设购买乙种树x棵,则购买甲种树2x棵,丙种树(1000﹣3x)棵,利用(1)中所求树木价格以及现计划用210000元资金购买这三种树共1000棵,得出等式方程,求出即可;(3)假设购买丙种树y棵,则甲、乙两种树共(1000﹣y)棵,根据题意得:200(1000﹣y)+300y≤210000+10120,求出即可.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )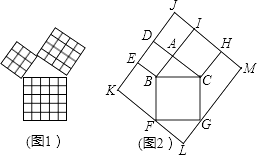
A.90
B.100
C.110
D.121
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明购买了一套安居型商品房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题:
(1)用含x、y的代数式表示地面总面积;
(2)若x=5,y=![]() ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘西自治州风景优美,物产丰富,一外地游客到某特产专营店,准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产.若购买3盒豆腐乳和2盒猕猴桃果汁共需180元;购买1盒豆腐乳和3盒猕猴桃果汁共需165元.
(1)请分别求出每盒豆腐乳和每盒猕猴桃果汁的价格;
(2)该游客购买了4盒豆腐乳和2盒猕猴桃果汁,共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形,这个黑色菱形可分割成n个边长为1的小三角形,若 ![]() =
= ![]() ,则△ABC的边长是 .
,则△ABC的边长是 . 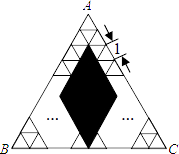
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业研制的产品今年第一季度的销售数量为300件,第二季度由于市场等因素,销售数量比第一季度减少了4%,从第三季度起,该企业搞了一系列的促销活动,销售数量又有所提升,第四季度的销售量达到了450件,假设第三季度与第四季度销售数量的增长率相同,求这个增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABO中,斜边AB=1.若OC∥BA,∠AOC=36°,则( ) 
A.点B到AO的距离为sin54°
B.点B到AO的距离为tan36°
C.点A到OC的距离为sin36°sin54°
D.点A到OC的距离为cos36°sin54°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD= ![]() .
. 
(1)求证:CD∥BF;
(2)求⊙O的半径;
(3)求弦CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com