
【题目】在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为 . 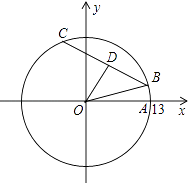
【答案】24
【解析】解:∵直线y=kx﹣3k+4=k(x﹣3)+4,
∴k(x﹣3)=y﹣4,
∵k有无数个值,
∴x﹣3=0,y﹣4=0,解得x=3,y=4,
∴直线必过点D(3,4),
∴最短的弦CB是过点D且与该圆直径垂直的弦,
∵点D的坐标是(3,4),
∴OD=5,
∵以原点O为圆心的圆过点A(13,0),
∴圆的半径为13,
∴OB=13,
∴BD=12,
∴BC的长的最小值为24;
故答案为:24.
根据直线y=kx﹣3k+4必过点D(3,4),求出最短的弦CB是过点D且与该圆直径垂直的弦,再求出OD的长,再根据以原点O为圆心的圆过点A(13,0),求出OB的长,再利用勾股定理求出BD,即可得出答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D, AB=AD.
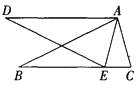
(1)试说明△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爸爸开车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下
时刻 | 9:00 | 9:45 | 12:00 |
碑上的数 | 是一个两位数,数字之和是9 | 十位与个位数字与9:00时所看到的正好相反 | 比9:00时看到的两位数中间多了个0 |
9:00时看到的两位数是( )
A. 54 B. 45 C. 36 D. 27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y= ![]() x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1 , 过点N1作直线l的垂线交x轴于点M2 , …;按此作法继续下去,则点M10的坐标为 .
x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1 , 过点N1作直线l的垂线交x轴于点M2 , …;按此作法继续下去,则点M10的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
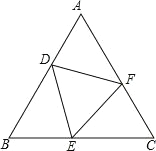
【题目】如图,△ABC 中,AB=AC,D、E、F 分别为 AB、BC、AC 上的点,且BD=CE,∠DEF=∠B.
(1)求证:∠BDE=∠CEF;
(2)当∠A=60°时,求证:△DEF 为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )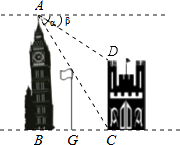
A.20米
B.10 ![]() 米
米
C.15 ![]() 米
米
D.5 ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x+1的图象与反比例函数 ![]() (k为常数,且k≠0)的图象都经过点A(m,2)
(k为常数,且k≠0)的图象都经过点A(m,2) 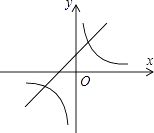
(1)求点A的坐标及反比例函数的表达式;
(2)结合图象直接比较:当x>0时,y1和y2的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com