
【题目】如图,一次函数y1=x+1的图象与反比例函数 ![]() (k为常数,且k≠0)的图象都经过点A(m,2)
(k为常数,且k≠0)的图象都经过点A(m,2) 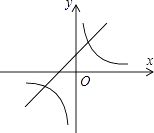
(1)求点A的坐标及反比例函数的表达式;
(2)结合图象直接比较:当x>0时,y1和y2的大小.
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE. 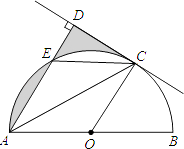
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是 ![]() 的中点,⊙O的半径为1,求图中阴影部分的面积.
的中点,⊙O的半径为1,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物体从P点运动到Q点所用时间为7秒,其运动速度v(米每秒)关于时间t(秒)的函数关系如图所示.某学习小组经过探究发现:该物体前进3秒运动的路程在数值上等于矩形AODB的面积.由物理学知识还可知:该物体前t(3<t≤7)秒运动的路程在数值上等于矩形AODB的面积与梯形BDNM的面积之和. 根据以上信息,完成下列问题: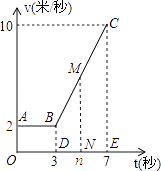
(1)当3<t≤7时,用含t的式子表示v;
(2)分别求该物体在0≤t≤3和3<t≤7时,运动的路程s(米)关于时间t(秒)的函数关系式;并求该物体从P点运动到Q总路程的 ![]() 时所用的时间.
时所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)![]() +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;
(2)如果(2+![]() )a-(1-
)a-(1-![]() )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC. 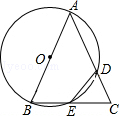
(1)求证:AB=AC;
(2)若AB=4,BC=2 ![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com