
【题目】若关于t的不等式组 ![]() ,恰有三个整数解,则关于x的一次函数
,恰有三个整数解,则关于x的一次函数 ![]() 的图象与反比例函数
的图象与反比例函数 ![]() 的图象的公共点的个数为 .
的图象的公共点的个数为 .
【答案】1或0
【解析】解:不等式组的解为:a≤t≤ ![]() , ∵不等式组恰有3个整数解,
, ∵不等式组恰有3个整数解,
∴﹣2<a≤﹣1.
联立方程组 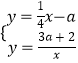 ,
,
得: ![]() x2﹣ax﹣3a﹣2=0,
x2﹣ax﹣3a﹣2=0,
△=a2+3a+2=(a+ ![]() )2﹣
)2﹣ ![]() =(a+1)(a+2)
=(a+1)(a+2)
这是一个二次函数,开口向上,与x轴交点为(﹣2,0)和(﹣1,0),对称轴为直线a=﹣ ![]() ,
,
其图象如下图所示: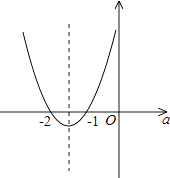
由图象可见:
当a=﹣1时,△=0,此时一元二次方程有两个相等的根,即一次函数与反比例函数有一个交点;
当﹣2<a<﹣1时,△<0,此时一元二次方程无实数根,即一次函数与反比例函数没有交点.
∴交点的个数为:1或0.
所以答案是:1或0.
【考点精析】本题主要考查了一元一次不等式组的整数解的相关知识点,需要掌握使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )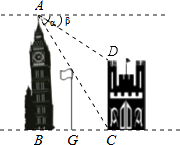
A.20米
B.10 ![]() 米
米
C.15 ![]() 米
米
D.5 ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其全等的依据是( )
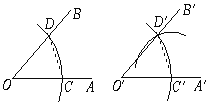
A.SAS B.ASA C.AAS D.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在图①中的正方形中剪去一个边长为2a+b的正方形,将剩余的部分按图②的方式拼成一个长方形.
(1)求剪去正方形的面积;
(2)求拼成的长方形的长、宽以及它的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x+1的图象与反比例函数 ![]() (k为常数,且k≠0)的图象都经过点A(m,2)
(k为常数,且k≠0)的图象都经过点A(m,2) 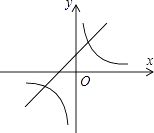
(1)求点A的坐标及反比例函数的表达式;
(2)结合图象直接比较:当x>0时,y1和y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P,Q两点停止运动.
(1)AC= cm,BC= cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,P与Q第一次相遇;
(4)当t为何值时,PQ=1cm.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题,
例题:若m2+2mn+2n2-6n+9=0,求m和n的值.
∵m2+2mn+2n2-6n+9=0
∴m2+2mn+n2+n2-6n+9=0
∴(m+n)2+(n-3)2=0
∴m+n=0,n-3=0
∴m=-3,n=3
问题(1)若x2+2y2-2xy-4y+4=0,求xy的值.
(2)已知a,b,c是△ABC的三边长,满足a2+b2-6a-6b+18+| 3-c |=0,请问△ABC是怎样形状的三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com