
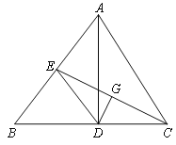
【题目】如图,△ABC中,AD是高,CE是中线,点G是CE的中点,且DG⊥CE,垂足为点G.
(1)求证:DC=BE;
(2)若∠AEC=54°,求∠BCE的度数.
【答案】(1)证明见解析(2)54°
【解析】
(1)由G是CE的中点,DG⊥CE得到DG是CE的垂直平分线,根据线段垂直平分线的性质得到DE=DC,由DE是Rt△ADB的斜边AB上的中线,根据直角三角形斜边上的中线等于斜边的一半得到DE=BE=![]() AB,即可得到DC=BE;
AB,即可得到DC=BE;
(2)由DE=DC得到∠DEC=∠BCE,由DE=BE得到∠B=∠EDB,根据三角形外角性质得到∠EDB=∠DEC+∠BCE=2∠BCE,则∠B=2∠BCE,由此根据外角的性质来求∠BCE的度数.
(1)∵G是CE的中点,DG⊥CE,
∴DG是CE的垂直平分线,
∴DE=DC,
∵AD是高,CE是中线,
∴DE是Rt△ADB的斜边AB上的中线,
∴DE=BE= ![]() AB,
AB,
∴DC=BE;
(2)∵DE=DC,
∴∠DEC=∠BCE,
∴∠EDB=∠DEC+∠BCE=2∠BCE,
∵DE=BE,
∴∠B=∠EDB,
∴∠B=2∠BCE,
∴∠AEC=3∠BCE=54°,则∠BCE=18°.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题: 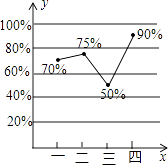
(1)若第一季度的汽车销售量为2100辆,求该季的汽车产量;
(2)圆圆同学说:“因为第二,第三这两个季度汽车销售数量占当季汽车产量是从75%降到50%,所以第二季度的汽车产量一定高于第三季度的汽车产量”,你觉得圆圆说的对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮在A点时测得灯塔C在它的北偏东42°方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55°方向上.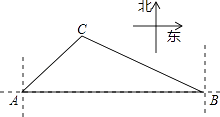
(1)求海轮在航行过程中与灯塔C的最短距离(结果精确到0.1);
(2)求海轮在B处时与灯塔C的距离(结果保留整数).
(参考数据:sin55°≈0.819,cos55°≈0.574,tan55°≈1.428,tan42°≈0.900,tan35°≈0.700,tan48°≈1.111)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点间的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )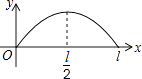
A.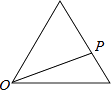
B.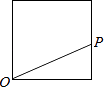
C.
D.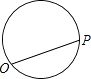
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
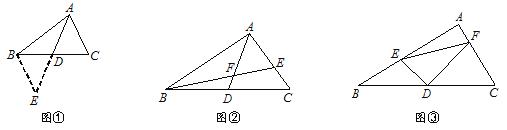
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
【灵活运用】
如图③,在△ABC中, ∠A=90°,D为BC中点, DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班毕业联欢会设计的即兴表演节目的摸球游戏,游戏采用一个不透明的盒子,里面装有五个分别标有数字1、2、3、4、5的乒乓球,这些球除数字外,其它完全相同,游戏规则是参加联欢会的50名同学,每人将盒子乒乓球摇匀后闭上眼睛从中随机一次摸出两个球(每位同学必须且只能摸一次).若两球上的数字之和是偶数就给大家即兴表演一个节目;否则,下个同学接着做摸球游戏,依次进行.
(1)用列表法或画树状图法求参加联欢会同学表演即兴节目的概率;
(2)估计本次联欢会上有多少个同学表演即兴节目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成). 安全知识测试成绩频数分布表
组别 | 成绩x(分数) | 组中值 | 频数(人数) |
1 | 90≤x<100 | 95 | 10 |
2 | 80≤x<90 | 85 | 25 |
3 | 70≤x<80 | 75 | 12 |
4 | 60≤x<70 | 65 | 3 |

(1)完成频数分布直方图;
(2)这个样本数据的中位数在第组;
(3)若将各组的组中值视为该组的平均成绩,则此次测试的平均成绩为;
(4)若将90分以上(含90分)定为“优秀”等级,则该县10000名初中生中,获“优秀”等级的学生约为人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com