
【题目】如图,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是两直线y1=2x+6、y2=2x﹣6中某条上的一点,若△APD是等腰Rt△,则点D的坐标为 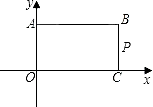
【答案】(4,2),(4,14),( ![]() ,
, ![]() ),(
),( ![]() ,
, ![]() )
)
【解析】解:易知:A(0,6),C(8,0),AB=8,OA=BC=6;
则点A正好位于直线y=2x+6上;
1)当点D位于直线y=2x+6上时,分三种情况:
①点P为直角顶点,结合图形,显然此时点D位于第四象限,不合题意;
②点D为直角顶点,那么∠DAP=45°,结合图形2可知:∠DAB>45°,
而点P位于线段BC上,故不存在这样的等腰直角三角形;
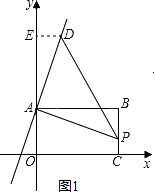
③点A为直角顶点,如图;
过D作DE⊥y轴于E,则△ADE≌△APB,得:AE=AB=8;
即点D的纵坐标为:14,代入y=2x+6中,可求得
点D(4,14);
2)当点D位于直线y=2x﹣6上时,分三种情况:
①点A为直角顶点,结合图形可知,此种情况显然不合题意;
②点D为直角顶点,分两种情况:
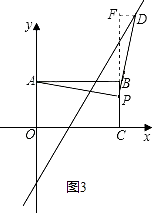
a、点D在矩形AOCB的内部时,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,设D(x,2x﹣6);
则OE=2x﹣6,AE=6﹣(2x﹣6)=12﹣2x,DF=EF﹣DE=8﹣x;
则△ADE≌△DPF,得DF=AE,即:
12﹣2x=8﹣x,x=4;
∴D(4,2);
b、点D在矩形AOCB的外部时,设D(x,2x﹣6);
则OE=2x﹣6,AE=OE﹣OA=2x﹣6﹣6=2x﹣12,DF=EF﹣DE=8﹣x;
同1可知:△ADE≌△DPFAE=DF,即:
2x﹣12=8﹣x,x= ![]() ;
;
∴D( ![]() ,
, ![]() );
);
③点P为直角顶点,显然此时点D位于矩形AOCB的外部;
设点D(x,2x﹣6),则CF=2x﹣6,BF=2x﹣6﹣6=2x﹣12;
易证得△APB≌△PDF,得:
AB=PF=8,PB=DF=x﹣8;
故BF=PF﹣PB=8﹣(x﹣8)=16﹣x;
联立两个表示BF的式子可得:
2x﹣12=16﹣x,即x= ![]() ;
;
∴D( ![]() ,
, ![]() );
);
综合上面六种情况可得:存在符合条件的等腰直角三角形;
且D点的坐标为:(4,2),(4,14),( ![]() ,
, ![]() ),(
),( ![]() ,
, ![]() ).
).



 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】2016年为更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如图的调查问卷(单选).在随机调查了某市全部10000名司机中的部分司机后,统计整理并制作了如下的统计图: 
根据以上信息解答下列问题:
(1)补全条形统计图,并计算扇形统计图中m=;
(2)该市支持选项C的司机大约有多少人?
(3)若要从该市支持选项C的司机中随机选择200名,给他们签订“永不酒驾”的保证书,则支持该选项的司机小李被选中的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. 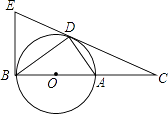
(1)求证:CD是⊙O的切线.
(2)过点B作⊙O的切线交CD的延长线于点E,若OB=5,BC=18,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用![]() 纸在某誊印社复印文件,复印页数不超过
纸在某誊印社复印文件,复印页数不超过![]() 时每页收费
时每页收费![]() 元;复印页数超过
元;复印页数超过![]() 时,超过部分每页收费
时,超过部分每页收费![]() 元.在某图书馆复印同样的文件,不论复印多少页,每页收费
元.在某图书馆复印同样的文件,不论复印多少页,每页收费![]() 元,如何根据复印的页数选择复印的地点使总价格比较便宜?
元,如何根据复印的页数选择复印的地点使总价格比较便宜?
查看答案和解析>>
科目:初中数学 来源: 题型:
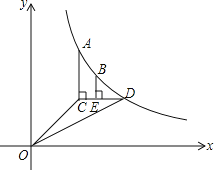
【题目】如图,已知函数![]() (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(1)求△OCD的面积;
(2)当BE=![]() AC时,求CE的长.
AC时,求CE的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据函数![]() (x>0)的图象经过点A(1,2),求函数解析式,再有AC∥y轴,AC=1求出C点坐标,然后根据CD∥x轴,求D点坐标,从而可求CD长,最后利用三角形面积公式求出△OCD的面积.
(x>0)的图象经过点A(1,2),求函数解析式,再有AC∥y轴,AC=1求出C点坐标,然后根据CD∥x轴,求D点坐标,从而可求CD长,最后利用三角形面积公式求出△OCD的面积.
(2)通过BE=![]() AC,求得B点坐标,进而求得CE长.
AC,求得B点坐标,进而求得CE长.
试题解析:解:(1)∵函数![]() (x>0)的图象经过点A(1,2),
(x>0)的图象经过点A(1,2),
∴![]() ,即k=2.
,即k=2.
∵AC∥y轴,AC=1,∴点C的坐标为(1,1).
∵ CD∥x轴,点D在函数图像上,∴点D的坐标为(2,1).
∴![]() .
.
(2)∵BE=![]() AC,∴BE=
AC,∴BE=![]() .
.
∵BE⊥CD,∴点B的纵坐标是![]() .∴点B的横坐标是
.∴点B的横坐标是![]() .
.
∴CE=![]() .
.
考点:1.反比例函数综合题;3.曲线上点的坐标与方程的关系;3.三角形的面积.
【题型】解答题
【结束】
27
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有 ![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得 ![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: +
,填空: + ![]() =( +
=( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.

(1)求证:AC∥DE;
(2)过点B作BF⊥AC于点F,连接EF,试判别四边形BCEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列单项式:![]() ,
,![]() ,
,![]() ,
,![]() ,…
,…![]() ,
,![]() ,…写出第
,…写出第![]() 个单项式,为了解这个问题,特提供下面的解题思路.
个单项式,为了解这个问题,特提供下面的解题思路.
![]() 这组单项式的系数的符号,绝对值规律是什么?
这组单项式的系数的符号,绝对值规律是什么?
![]() 这组单项式的次数的规律是什么?
这组单项式的次数的规律是什么?
![]() 根据上面的归纳,你可以猜想出第
根据上面的归纳,你可以猜想出第![]() 个单项式是什么?
个单项式是什么?
![]() 请你根据猜想,请写出第
请你根据猜想,请写出第![]() 个,第
个,第![]() 个单项式.
个单项式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com