
【题目】如图,在平行四边形ABCD中,AB⊥AC,AB=1,BC=![]() ,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转分别交BC、AD于点E、F.
,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转分别交BC、AD于点E、F.
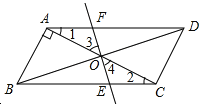
(1)试说明在旋转过程中,AF与CE总保持相等;
(2)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,求出此时AC绕点O顺时针旋转的角度.
【答案】(1)证明见解析;(2)证明见解析;(3)45°.
【解析】
试题分析:(1)根据平行四边形的对边平行可得AD∥BC,对角线互相平分可得OA=OC,再根据两直线平行,内错角相等求出∠1=∠2,然后利用“角边角”证明△AOF和△COE全等,根据全等三角形对应边相等即可得到AF=CE;
(2)根据垂直的定义可得∠BAO=90°,然后求出∠BAO=∠AOF,再根据内错角相等,两直线平行可得AB∥EF,然后根据平行四边形的对边平行求出AF∥BE,再根据两组对边分别平行的四边形是平行四边形证明;
(3)根据(1)的结论可得AF=CE,再求出DF∥BE,DF=BE,然后根据一组对边平行且相等的四边形是平行四边形求出四边形BEDF平行四边形,再求出对角线互相垂直的平行四边形是菱形可得EF⊥BD时,四边形BEDF是菱形;根据勾股定理列式求出AC=2,再根据平行四边形的对角线互相平分求出AO=1,然后求出∠AOB=45°,再根据旋转的定义求出旋转角即可.
试题解析:(1)在ABCD中,AD∥BC,OA=OC,
∴∠1=∠2,
在△AOF和△COE中,
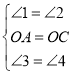 ,
,
∴△AOF≌△COE(ASA),
∴AF=CE;
(2)由题意,∠AOF=90°(如图2),
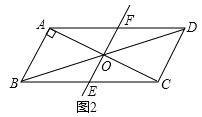
又∵AB⊥AC,
∴∠BAO=90°,
∠AOF=90°,
∴∠BAO=∠AOF,
∴AB∥EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
即:AF∥BE,
∵AB∥EF,AF∥BE,
∴四边形ABEF是平行四边形;
(3)当EF⊥BD时,四边形BEDF是菱形(如图3).
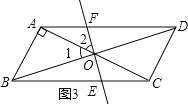
∵ABCD,AF=CE,
∴AD∥BC,AD=BC,
∴DF∥BE,DF=BE,
∴四边形BEDF是平行四边形,
又∵EF⊥BD,
∴BEDF是菱形,
∵AB⊥AC,
∴在△ABC中,∠BAC=90°,
∴BC2=AB2+AC2,
∵AB=1,BC=![]() ,
,
∴AC=![]() =
=![]() =2,
=2,
∵四边形ABCD是平行四边形,
∴OA=![]() AC=
AC=![]() ×2=1,
×2=1,
∵在△AOB中,AB=AO=1,∠BAO=90°,
∴∠1=45°,
∵EF⊥BD,
∴∠BOF=90°,
∴∠2=∠BOF-∠1=90°-45°=45°,
即:旋转角为45°.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
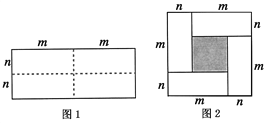
(1)请用两种不同的方法求图2中阴影部分的面积.
方法1: ;
方法2: ;
(2)观察图2请你写出下列三个代数式:(m+n)2,(m-n)2,mn之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:![]() ,
,![]() ,求:
,求:![]() 的值;
的值;
②已知:![]() ,
,![]() ,求:
,求:![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
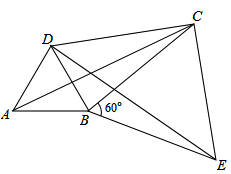
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.
①求证:△BCE是等边三角形;
②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太平洋服装超市某种服装的标价为120元,元旦期间以九折降价出售,仍获利20%,该服装的进货价为( )
A.80元
B.85元
C.90元
D.95元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保证中小学生每天锻炼一小时,句容某中学开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的统计图(1)和图(2).
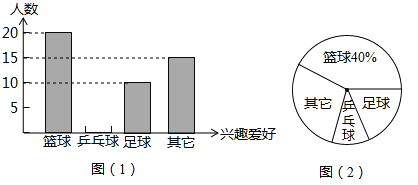
(1)某班同学的总人数为 人;
(2)请根据所给信息在图(1)中将表示“乒乓球”项目的图形补充完整;
(3)扇形统计图(2)中表示”篮球”项目扇形的圆心角度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测算一块600亩试验田里新培育的杂交水稻的产量,随机对其中的10亩杂交水稻的产量进行了检测,在这个问题中10是( )
A. 个体 B. 总体 C. 总体的样本 D. 样本容量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
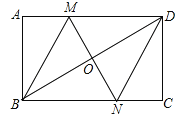
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com