
如图,在平面直角坐标系中,己知点O(0,0),A(5,0),B(4,4).
(1)求过O、B、A三点的抛物线的解析式.
(2)在第一象限的抛物线上存在点M,使以O、A、B、M为顶点的四边形面积最大,求点M的坐标.
(3)作直线x=m交抛物线于点P,交线段OB于点Q,当△PQB为等腰三角形时,求m的值.

(1)该抛物线的解析式为y=﹣x(x﹣5)=﹣x2+5x;
(2)M(2,6);
(3)当△PQB为等腰三角形时,m的值为1,2或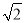 .
.
【解析】
试题分析:(1)由于抛物线与x轴的两个交点已知,因此抛物线的解析式可设成交点式,然后把点B的坐标代入,即可求出抛物线的解析式;
(2)以O、A、B、M为顶点的四边形中,△OAB的面积固定,因此只要另外一个三角形面积最大,则四边形面积即最大;求出另一个三角形面积的表达式,利用二次函数的性质确定其最值;本问需分类讨论:
①当0<x≤4时,点M在抛物线OB段上时,如答图1所示;
②当4<x≤5时,点M在抛物线AB段上时,图略.
(3)△PQB为等腰三角形时,有三种情形,需要分类讨论,避免漏【解析】
①若点B为顶点,即BP=BQ,如答图2﹣1所示;
②若点P为顶点,即PQ=PB,如答图2﹣2所示;
③若点P为顶点,即PQ=QB,如答图2﹣3所示.
试题解析:(1)∵该抛物线经过点A(5,0),O(0,0),
∴该抛物线的解析式可设为y=a(x﹣0)(x﹣5)=ax(x﹣5).
∵点B(4,4)在该抛物线上,
∴a×4×(4﹣5)=4.
∴a=﹣1.
∴该抛物线的解析式为y=﹣x(x﹣5)=﹣x2+5x;
(2)以O、A、B、M为顶点的四边形中,△OAB的面积固定,因此只要另外一个三角形面积最大,则四边形面积即最大.
①当0<x≤4时,点M在抛物线OB段上时,如答图1所示.
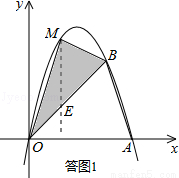
∵B(4,4),∴易知直线OB的解析式为:y=x.
设M(x,﹣x2+5x),
过点M作ME∥y轴,交OB于点E,则E(x,x),
∴ME=(﹣x2+5x)﹣x=﹣x2+4x.
S△OBM=S△MEO+S△MEB=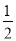 ME(xE﹣0)+
ME(xE﹣0)+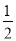 ME(xB﹣xE)=
ME(xB﹣xE)=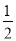 ME•xB=
ME•xB=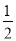 ME×4=2ME,
ME×4=2ME,
∴S△OBM=﹣2x2+8x=﹣2(x﹣2)2+8
∴当x=2时,S△OBM最大值为8,即四边形的面积最大.
②当4<x≤5时,点M在抛物线AB段上时,
可求得直线AB解析式为:y=﹣4x+20.
设M(x,﹣x2+5x),
过点M作ME∥y轴,交AB于点E,则E(x,﹣4x+20),
∴ME=(﹣x2+5x)﹣(﹣4x+20)=﹣x2+9x﹣20.
S△ABM=S△MEB+S△MEA=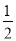 ME(xE﹣xB)+
ME(xE﹣xB)+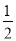 ME(xA﹣xE)=
ME(xA﹣xE)=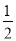 ME•(xA﹣xB)=
ME•(xA﹣xB)=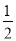 ME×1=
ME×1=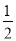 ME,
ME,
∴S△ABM=﹣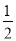 x2+
x2+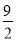 x﹣10=﹣
x﹣10=﹣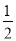 (x﹣
(x﹣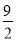 )2+
)2+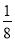
∴当x=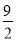 时,S△ABM最大值为
时,S△ABM最大值为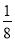 ,即四边形的面积最大.
,即四边形的面积最大.
比较①②可知,当x=2时,四边形面积最大.
当x=2时,y=﹣x2+5x=6,
∴M(2,6);
(3)由题意可知,点P在线段OB上方的抛物线上.
设P(m,﹣m2+5m),则Q(m,m)
当△PQB为等腰三角形时,
①若点B为顶点,即BP=BQ,如答图2﹣1所示.
过点B作BE⊥PQ于点E,则点E为线段PQ中点,
∴E(m,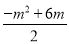 ).
).
∵BE∥x轴,B(4,4),
∴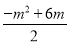 =4,
=4,
解得:m=2或m=4(与点B重合,舍去)
∴m=2;
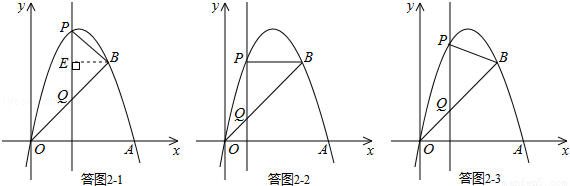
②若点P为顶点,即PQ=PB,如答图2﹣2所示.
易知∠BOA=45°,∴∠PQB=45°,则△PQB为等腰直角三角形.
∴PB∥x轴,
∴﹣m2+5m=4,
解得:m=1或m=4(与点B重合,舍去)
∴m=1;
③若点P为顶点,即PQ=QB,如答图2﹣3所示.
∵P(m,﹣m2+5m),Q(m,m),
∴PQ=﹣m2+4m.
又∵QB=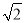 (xB﹣xQ)=
(xB﹣xQ)=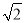 (4﹣m),
(4﹣m),
∴﹣m2+4m=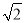 (4﹣m),
(4﹣m),
解得:m=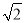 或m=4(与点B重合,舍去),
或m=4(与点B重合,舍去),
∴m=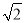 .
.
综上所述,当△PQB为等腰三角形时,m的值为1,2或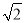 .
.
考点:二次函数综合题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源:2014年初中毕业升学考试(安徽卷)数学(解析版) 题型:选择题
某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如右表,则棉花纤维长度的数据在8≤x<32这个范围的频率为( )
棉花纤维长度x | 频数 |
0≤x<8 | 1 |
8≤x<16 | 2 |
16≤x<24 | 8 |
24≤x<32 | 6 |
32≤x<40 | 3 |
A.0.8 B.0.7 C.0.4 D.0.2
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川雅安卷)数学(解析版) 题型:选择题
如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE= ,则正方形的面积为( )
,则正方形的面积为( )

A.5 B.4 C.3 D.2
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川达州卷)数学(解析版) 题型:解答题
某服装商预测一种应季衬衫能畅销市场,就用8000元购进一批衬衫,面市后果然供不应求,服装商又用17600元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了8元.商家销售这种衬衫时每件定价都是100元,最后剩下10件按8折销售,很快售完.在这两笔生意中,商家共盈利多少元?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川达州卷)数学(解析版) 题型:填空题
《庄子.天下篇》中写道:“一尺之棰,日取其半,万世不竭”意思是:一根一尺的木棍,如果每天截取它的一半,永远也取不完,如图.

由图易得: = .
= .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川资阳卷)数学(解析版) 题型:解答题
如图,一次函数y=kx+b(k≠0)的图象过点P(﹣ ,0),且与反比例函数y=
,0),且与反比例函数y=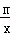 (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川眉山卷)数学(解析版) 题型:选择题
一组数据如下:3,6,7,2,3,4,3,6,那么这组数据的中位数和众数分别是( )
A.3,3 B.3.5,3 C.4,3 D.3.5,6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com