
如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE= ,则正方形的面积为( )
,则正方形的面积为( )

A.5 B.4 C.3 D.2
B
【解析】
试题分析:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,

∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵四边形ABCD是正方形,
∴∠COD=90° OC=OD,
∴∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
又∵∠N=∠CMO=90°,
∴△COM≌△DON(AAS),
∴OM=ON,
∴四边形OMEN是正方形,
设正方形ABCD的边长为2a,则OC=OD=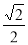 ×2a=
×2a=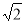 a,
a,
∵∠CED=90°,∠DCE=30°,
∴DE=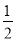 CD=a,
CD=a,
∴CE= ,
,
∴S四边形OCED=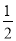 a•
a•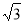 a+
a+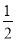 •(
•(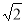 a)•(
a)•(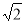 a)=
a)=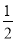 ×(
×(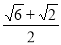 )2,
)2,
∴a2=1,
∴S正方形ABCD=(2a)2=4a2=4×1=4.
故选B.
考点:1、正方形的性质;2、全等三角形的判定与性质;3、勾股定理.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源:2014年初中毕业升学考试(安徽卷)数学(解析版) 题型:解答题
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
(1)将△ABC向上平移3个单位得到△A1B1C1,请画出△A1B1C1;
(2)请画一个格点△A2B2C2,使△A2B2C2∽△ABC,且相似比不为1.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川雅安卷)数学(解析版) 题型:解答题
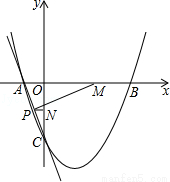
如图,直线y=﹣3x﹣3与x轴、y轴分别相交于点A、C,经过点C且对称轴为x=1的抛物线y=ax2+bx+c与x轴相交于A、B两点.
(1)试求点A、C的坐标;
(2)求抛物线的解析式;
(3)若点M在线段AB上以每秒1个单位长度的速度由点B向点A运动,同时,点N在线段OC上以相同的速度由点O向点C运动(当其中一点到达终点时,另一点也随之停止运动),又PN∥x轴,交AC于P,问在运动过程中,线段PM的长度是否存在最小值?若有,试求出最小值;若无,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川雅安卷)数学(解析版) 题型:填空题
关于x的方程x2﹣(2m﹣1)x+m2﹣1=0的两实数根为x1,x2,且x12+x22=3,则m= .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川达州卷)数学(解析版) 题型:解答题
如图,在平面直角坐标系中,己知点O(0,0),A(5,0),B(4,4).
(1)求过O、B、A三点的抛物线的解析式.
(2)在第一象限的抛物线上存在点M,使以O、A、B、M为顶点的四边形面积最大,求点M的坐标.
(3)作直线x=m交抛物线于点P,交线段OB于点Q,当△PQB为等腰三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川达州卷)数学(解析版) 题型:填空题
直线y=kx+b不经过第四象限,则( )
A.k>0,b>0 B.k<0,b>0 C.k≥0,b≥0 D.k<0,b≥0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com