
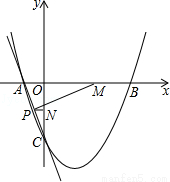
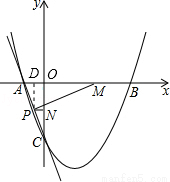
��ͼ��ֱ��y=��3x��3��x�ᡢy��ֱ��ཻ�ڵ�A��C��������C�ҶԳ���Ϊx=1��������y=ax2+bx+c��x���ཻ��A��B���㣮
��1�������A��C�����ꣻ
��2���������ߵĽ���ʽ��
��3������M���߶�AB����ÿ��1����λ���ȵ��ٶ��ɵ�B���A�˶���ͬʱ����N���߶�OC������ͬ���ٶ��ɵ�O���C�˶���������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶�������PN��x�ᣬ��AC��P�������˶������У��߶�PM�ij����Ƿ������Сֵ�����У��������Сֵ�����ޣ���˵�����ɣ�
��1��A����1��0����C��0����3����
��2�������ߵĽ���ʽΪy=x2��2x��3��
��3�����˶������У��߶�PM�ij��ȴ�����Сֵ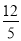 ��
��
��������
�����������1����ֱ�߽���ʽy=��3x��3����y=0�������x��ֵ���õ�ֱ����x�ύ��A�����꣬��x=0�������y��ֵ���õ�ֱ����y�ύ��C�����ꣻ
��2������������y=ax2+bx+c�ĶԳ���Ϊx=1���ҹ���A����1��0����C��0����3�����ɵõ������飬�ⷽ���鼴����������ߵĽ���ʽ��
��3���ɶԳ��Եõ�B��3��0�������M�˶���ʱ��Ϊt�루0��t��3������M��3��t��0����N��0����t����P��xP����t������ɵ�xP���ٹ���P��PD��x���ڵ�D����D����1��0�����ڡ�PDM�����ù��ɶ����ó�PM2=MD2+PD2=����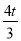 +4��2+����t��2=
+4��2+����t��2=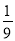 ��25t2��96t+144�������ö��κ��������ʿ�֪��t=
��25t2��96t+144�������ö��κ��������ʿ�֪��t=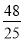 ʱ��PM2��СֵΪ
ʱ��PM2��СֵΪ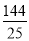 �������˶������У��߶�PM�ij��ȴ�����Сֵ
�������˶������У��߶�PM�ij��ȴ�����Сֵ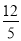 ��
��
�����������1����y=��3x��3��
�൱y=0ʱ����3x��3=0�����x=��1��
��A����1��0����
�ߵ�x=0ʱ��y=��3��
��C��0����3����
��2����������y=ax2+bx+c�ĶԳ���Ϊx=1������A����1��0����C��0����3����
��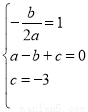 �����
�����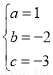 ��
��
�������ߵĽ���ʽΪy=x2��2x��3��
��3���ɶԳ��Եõ�B��3��0�������M�˶���ʱ��Ϊt�루0��t��3������M��3��t��0����N��0����t����P��xP����t����
��-t=-3xp-3
xp=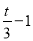 ��
��
����P��PD��x���ڵ�D����D��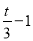 ��0����
��0����
��MD=��3��t������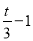 ��=��
��=��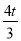 +4��
+4��
��PM2=MD2+PD2=����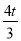 +4��2+����t��2=
+4��2+����t��2=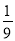 ��25t2��96t+144����
��25t2��96t+144����
�֡ߩ�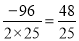 ��3��
��3��
�൱t=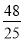 ʱ��PM2��СֵΪ
ʱ��PM2��СֵΪ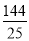 ��
��
�����˶������У��߶�PM�ij��ȴ�����Сֵ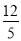 ��
��
���㣺1��һ�κ���ͼ���ϵ������������2������ϵ������3�����ɶ�����4�����κ���������


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�ɽ�����ݾ�����ѧ�������棩 ���ͣ������
��ͼ������ABCD�У�AB=20��BC=10����PΪAB����һ���㣬DP��AC�ڵ�Q.
��1����֤����APQ����CDQ��
��2��P���A�������AB����ÿ��1����λ���ٶ���B���ƶ����ƶ�ʱ��Ϊt��.
����tΪ��ֵʱ��DP��AC��
���� ��д��y��t֮��ĺ�������ʽ����̽��P���˶����ڼ��뵽�ڼ���֮��ʱ��yȡ����Сֵ.
��д��y��t֮��ĺ�������ʽ����̽��P���˶����ڼ��뵽�ڼ���֮��ʱ��yȡ����Сֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�ɽ������������ѧ�������棩 ���ͣ�ѡ����
�������г�ȡһ����������Ϊ����ȥ���������ij������.����������ȷ������ ��
A.��������Խ������ƽ������Խ��
B.��������Խ�������������Խ��
C.��������Խ���������ļ����Խ��
D.��������Խ������Ĺ��ƾ�Խȷ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ����վ�����ѧ�������棩 ���ͣ������
ij������һ�·��²�Ʒ���з��ʽ�ΪaԪ���Ժ�ÿ���²�Ʒ���з��ʽ���������������ʶ���x����ó��������·��²�Ʒ���з��ʽ�y��Ԫ������x�ĺ�����ϵʽΪy= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ����վ�����ѧ�������棩 ���ͣ�ѡ����
ij�ij�Ϊ�˽�һ���������������������ȡ��20������ά���в������䳤��x����λ��mm�������ݷֲ����ұ���������ά���ȵ�������8��x��32�����Χ��Ƶ��Ϊ�� ��
����ά����x | Ƶ�� |
0��x��8 | 1 |
8��x��16 | 2 |
16��x��24 | 8 |
24��x��32 | 6 |
32��x��40 | 3 |
A��0.8 B��0.7 C��0.4 D��0.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ��Ű�������ѧ�������棩 ���ͣ������
ij��ʦ�Ա�������ѧ������ѧ���Գɼ����ɼ�Ϊ����������Ϊ100�֣�����ͳ�Ʒ��������Ƴ�����Ƶ����Ƶ�ʷֲ�����Ƶ���ֲ�ֱ��ͼ���������ͼ���ṩ����Ϣ������������⣺
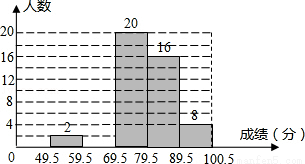
���� | 49.5��59.5 | 59.5��69.5 | 69.5��79.5 | 79.5��89.5 | 89.5��100.5 |
Ƶ�� | 2 | a | 20 | 16 | 8 |
Ƶ�� | 0.04 | 0.08 | 0.40 | 0.32 | b |
��1����a��b��ֵ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����ʦ���ӳɼ�������80�ֵ�ѧ����ѡ1�˽���ѧϰ���飬��ô��ѡ�е�ѧ����ɼ�������90�ֵĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ��Ű�������ѧ�������棩 ���ͣ�ѡ����
��ͼ��ABCDΪ�����Σ�OΪAC��BD�Ľ��㣬��DCEΪRt������CED=90�㣬��DCE=30�㣬��OE= ���������ε����Ϊ��������
��������������������

A��5 B��4 C��3 D��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ����ݾ�����ѧ�������棩 ���ͣ������
ij��װ��Ԥ��һ��Ӧ�������ܳ����г�������8000Ԫ����һ�����������к��Ȼ����Ӧ��װ������17600Ԫ�����˵ڶ������ֳ��������������ǵ�һ������������2���������۹���8Ԫ���̼��������ֳ���ʱÿ�����۶���100Ԫ�����ʣ��10����8�����ۣ��ܿ����꣮�������������У��̼ҹ�ӯ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ�����������ѧ�������棩 ���ͣ�ѡ����
����������ȷ���ǣ�������
A��a3+a4=a7 B��2a3•a4=2a7 C����2a4��3=8a7 D��a8��a2=a4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com