
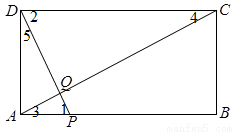
如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位的速度向B点移动,移动时间为t秒.
①当t为何值时,DP⊥AC?
②设 ,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.

(1)证明见解析;(2)①5;②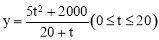 ,8-9.
,8-9.
【解析】
试题分析:(1)如图,由矩形的性质求出∠1=∠2,∠3=∠4即可证明△APQ∽△CDQ.
(2)①当DP⊥AC时,由△ADC∽△PAD列比例式可求解.
②根据相似,求出两个三角形的高(用t的代数式表示),即可求出y与t之间的函数解析式;列表求出函数值得出P点运动到第8秒到第9秒之间时,y取得最小值.
试题解析:(1)如图,∵四边形ABCD是矩形,∴AB∥CD. ∴∠1=∠2,∠3=∠4.
∴△APQ∽△CDQ.
(2)①当DP⊥AC时,∴∠4+∠2=90 o.
又∵∠5+∠2=90 o,∴∠4=∠5.
又∵∠ADC=∠DAP=90 o,∴△ADC∽△PAD.∴ ,即
,即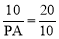 .∴PA=5.
.∴PA=5.
∵P点从A点出发沿AB边以每秒1个单位的速度向B点移动,∴t=5.
②设△APQ的边AP上的高为h,则△DCQ的边上的高为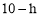 .
.
∵由(1)△APQ∽△CDQ,∴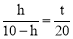 .∴
.∴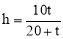 .∴
.∴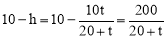 .
.
∴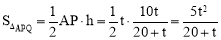 ,
,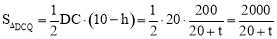 .
.
∴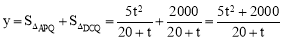 .
.
∴y与t之间的函数解析式为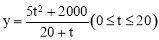 .
.
给出t的部分取值,计算出y的对应值列表如下:
t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
y | 100 | 95.48 | 91.88 | 88.91 | 86.67 | 85 | 83.85 | 83.15 | 82.86 | 82.93 | 83.33 |
t | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|
y | 84.03 | 85 | 86.21 | 87.65 | 89.29 | 93.11 | 95.26 | 97.56 | 100 |
|
|
从表中可看出:
当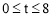 时;y随t的值的增大而减小;当
时;y随t的值的增大而减小;当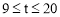 时;y随t的值的增大而增大.
时;y随t的值的增大而增大.
∴P点运动到第8秒到第9秒之间时,y取得最小值.
考点:1.单动点问题;2.相似三角形的判定和性质;3.由实际问题列函数关系式;4.列表求函数值分析函数的性质.


科目:初中数学 来源:2014年初中毕业升学考试(广西北海卷)数学(解析版) 题型:解答题
已知△ABC中,∠A=25°,∠B=40°.
(1)求作:⊙O,使得⊙O经过A、C两点,且圆心O落在AB边上.(要求尺规作图,保留作图痕迹,不必写作法)
(2)求证:BC是(1)中所作⊙O的切线.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:选择题
如图,把一块含有45°角的直角三角板两个顶点放在直尺的对边上,如果∠1=20°,则∠2的度数是( )

A、15° B、20° C、25° D、30°
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(山东济宁卷)数学(解析版) 题型:解答题
山东省第二十三届运动会将于2014年在济宁举行.下图是某大学未制作完整的三个年级省运会志愿者的统计图,请你根据图中所给信息解答下列问题:

(1)请你求出三年级有多少名省运会志愿者,并将两幅统计图补充完整;
(2)要求从一年级、三年级志愿者中各推荐一名队长候选人,二年级志愿者中推荐两名队长候选人,四名候选人中选出两人任队长,用列表法或树形图,求出两名队长都是二年级志愿者的概率是多少?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川雅安卷)数学(解析版) 题型:解答题
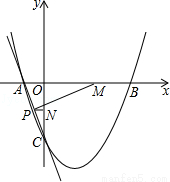
如图,直线y=﹣3x﹣3与x轴、y轴分别相交于点A、C,经过点C且对称轴为x=1的抛物线y=ax2+bx+c与x轴相交于A、B两点.
(1)试求点A、C的坐标;
(2)求抛物线的解析式;
(3)若点M在线段AB上以每秒1个单位长度的速度由点B向点A运动,同时,点N在线段OC上以相同的速度由点O向点C运动(当其中一点到达终点时,另一点也随之停止运动),又PN∥x轴,交AC于P,问在运动过程中,线段PM的长度是否存在最小值?若有,试求出最小值;若无,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com