

分析 (1)根据分母不能等于零,可以解答本题;
(2)根据函数解析式可以判断函数图象所在的位置,本题得以解决;
(3)根据题目中的解答过程可以将没写的补充完整;
(4)根据(3)的特点可以解答本题.
解答 解:(1)∵y=x+$\frac{4}{x}$,
∴x≠0,
故答案为:x≠0;
(2)∵y=x+$\frac{4}{x}$,
∴x>0时,y>0,
当x<0时,y<0,故选项B、D错误,
∵x≠0,∴选项A错误,
故选C;
(3)解:∵x>0
∴y=x+$\frac{4}{x}$
=($\sqrt{x}$)2+($\frac{2}{\sqrt{x}}$)2
=($\sqrt{x}$-$\frac{2}{\sqrt{x}}$)2+2
∵($\sqrt{x}$-$\frac{2}{\sqrt{x}}$)2≥0,
∴y≥2,
故答案为:2,2;
(4)y=$\frac{{x}^{2}+5x+4}{x}$=x+5+$\frac{4}{x}$=(x+$\frac{4}{x}$)+5≥7,
故答案为:y≥7.
点评 本题考查二次函数的性质、一次函数图象上点的特征、二次函数的图象,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,∠ACB=90°,O为边AB上的一点,以O为圆心,以OA为半径,作⊙O,交AB于点D,交AC于点E,交BC于点F,且点F恰好是ED的中点,连接DF.
在△ABC中,∠ACB=90°,O为边AB上的一点,以O为圆心,以OA为半径,作⊙O,交AB于点D,交AC于点E,交BC于点F,且点F恰好是ED的中点,连接DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
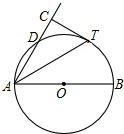 如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.
如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC在方格纸中,设单元格边长为1.
如图,△ABC在方格纸中,设单元格边长为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
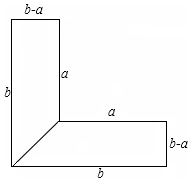 李红的叔叔在郊区种菜,他家有一块L形菜地,要把L形菜地按如图所示的那样分成面积相等的两个梯形,种上不同的蔬菜.这两个梯形的上底都是a米,下底都是b米,高都是(b-a)米.
李红的叔叔在郊区种菜,他家有一块L形菜地,要把L形菜地按如图所示的那样分成面积相等的两个梯形,种上不同的蔬菜.这两个梯形的上底都是a米,下底都是b米,高都是(b-a)米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com