
【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(探究展示)
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
(拓展延伸)
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.

【答案】(1)证明见解析;(2)AM=DE+BM成立,证明见解析;(3)①结论AM=AD+MC仍然成立;②结论AM=DE+BM不成立.
【解析】
(1)从平行线和中点这两个条件出发,延长AE、BC交于点N,易证△ADE≌△NCE,得到AD=CN,再证明AM=NM即可;(2)过点A作AF⊥AE,交CB的延长线于点F,
易证△ABF≌△ADE,从而证明AM=FM,即可得证;(3)AM=DE+BM需要四边形ABCD是正方形,故不成立,AM=AD+MC仍然成立.
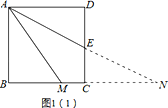
(1)延长AE、BC交于点N,如图1(1),
∵四边形ABCD是正方形,∴AD∥BC.∴∠DAE=∠ENC.
∵AE平分∠DAM,∴∠DAE=∠MAE.∴∠ENC=∠MAE.∴MA=MN.
在△ADE和△NCE中,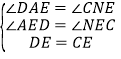
∴△ADE≌△NCE(AAS).∴AD=NC.∴MA=MN=NC+MC=AD+MC.
(2)AM=DE+BM成立.
证明:过点A作AF⊥AE,交CB的延长线于点F,如图1(2)所示.
∵四边形ABCD是正方形,∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC.
∵AF⊥AE,∴∠FAE=90°.∴∠FAB=90°﹣∠BAE=∠DAE.
在△ABF和△ADE中,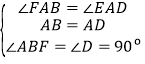
∴△ABF≌△ADE(ASA).
∴BF=DE,∠F=∠AED.
∵AB∥DC,
∴∠AED=∠BAE.
∵∠FAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠FAB=∠FAM.
∴∠F=∠FAM.
∴AM=FM.
∴AM=FB+BM=DE+BM.
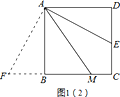
(3)①结论AM=AD+MC仍然成立.②结论AM=DE+BM不成立.


科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(4,0),点B从原点出发,沿y轴负方向以每秒1个单位长度的速度运动,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBE,等腰Rt△ABF,连结EF交y轴于P点,当点B在y轴上运动时,经过t秒时,点E的坐标是_____(用含t的代数式表示),PB的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B、C两人中的某一人,以后的每一次传球都是由上次的接球者将球随机地传给其他两人中的某一人.(画出树状图或列表)
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,
(1)若半径为1的⊙O经过点A、B、D,且∠A=60°,求此时菱形的边长;
(2)若点P为AB上一点,把菱形ABCD沿过点P的直线a折叠,使点D落在BC边上,利用无刻度的直尺和圆规作出直线a.(保留作图痕迹,不必说明作法和理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据说我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题: 一个数是 59319,希望求出它的立方根.华罗庚脱口而出:39. 邻座的乘客十分惊奇,忙问计算的奥妙. 你知道华罗庚是怎样计算的吗?请按照下面的问题试一试:
(1)由![]() ,试确定
,试确定![]() 是 __________位数;
是 __________位数;
(2)由 19683 个位数是 3,试确定![]() 个位数是 ________________;
个位数是 ________________;
(3)如果划去 19683 后面的三位数 683 得到数 19 ,而![]() ,由此你能确定
,由此你能确定![]() 十位 的数字是___________ ;
十位 的数字是___________ ;
(4) 用上述方法确定 110592 的立方根是_______________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上有点![]() ,
,![]() ,
,![]() ,它们表示的数分别为
,它们表示的数分别为![]() ,
,![]() ,
,![]() ,且满足:
,且满足:![]() ;
;![]() ,
,![]() ,
,![]() 三点同时出发沿数轴向右运动,它们的速度分别为:
三点同时出发沿数轴向右运动,它们的速度分别为:![]() (单位/秒),
(单位/秒),![]() (单位/秒),
(单位/秒),![]() (单位/秒).
(单位/秒).
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)运动时间![]() 等于多少时,
等于多少时,![]() 点与
点与![]() 点、
点、![]() 点的距离相等?
点的距离相等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com