
【题目】如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=![]() ,BC=
,BC=![]() ,CD=4,则AD边的长为_____________.
,CD=4,则AD边的长为_____________.

【答案】2![]()
【解析】
作AE⊥BC,DF⊥BC,构建直角△ AEB和直角△DFC,在直角三角形中求出 BE,CF,DF,从而求出EF和DG的值,进而求出AD.
解:如图:过点A、D分别作AE、DF垂直于直线BC,垂足分别为E、F,
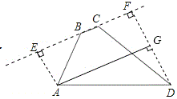
∵∠ABC=135°,
∴∠EBA=45°,
∴BE=AE,
∵AB=![]() ,AB2=BE2+AE2,
,AB2=BE2+AE2,
∴BE=AE=![]() ,
,
∵∠BCD=120°,
∴∠FCD=60°,∠CDF=30°
又∵CD=4,
∴CF=2,DF=2![]() ,
,
∴EF=EB+BC+CF=![]() =5,
=5,
过点A作AG⊥DF,垂足为G,
∴四边形AEFG是矩形,
∴GF=AE=![]() ,AG=EF=5,则DG=DF-GF=
,AG=EF=5,则DG=DF-GF=![]() ,
,
在RT△AGD中,根据勾股定理可得AD=![]() .
.
故本题答案为:2![]() .
.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车油箱中的余油量![]() (升
(升![]() 是它行驶的时间
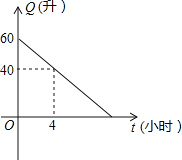
是它行驶的时间![]() (小 时) 的一次函数 . 某天该汽车外出时, 油箱中余油量与行驶时间的变化关系如图:
(小 时) 的一次函数 . 某天该汽车外出时, 油箱中余油量与行驶时间的变化关系如图:
(1) 根据图象, 求油箱中的余油![]() 与行驶时间
与行驶时间![]() 的函数关系 .
的函数关系 .
(2) 从开始算起, 如果汽车每小时行驶 40 千米, 当油箱中余油 20 升时, 该汽车行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(探究展示)
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
(拓展延伸)
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法: ① ![]() ;②数轴上的点与实数成一一对应关系;③两条直线被第三条直线所截,同位角相等;④垂直于同一条直线的两条直线互相平行;⑤两个无理数的和还是无理数;⑥无理数都是无限小数,其中正确的个数有 ___________
;②数轴上的点与实数成一一对应关系;③两条直线被第三条直线所截,同位角相等;④垂直于同一条直线的两条直线互相平行;⑤两个无理数的和还是无理数;⑥无理数都是无限小数,其中正确的个数有 ___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,欢欢一家随旅游团到某风景区旅游,集体门票的收费标准是: ![]() 人以内(含
人以内(含![]() 人),每人
人),每人![]() 元;超过
元;超过![]() 人的,超过的部分每人
人的,超过的部分每人![]() 元.
元.
(![]() )写出应收门票费
)写出应收门票费![]() (元)与游览人数
(元)与游览人数![]() (人)(其中
(人)(其中![]() )之间的关系式.
)之间的关系式.
(![]() )利用(
)利用(![]() )中的关系式计算:若欢欢一家所在的旅游团共
)中的关系式计算:若欢欢一家所在的旅游团共![]() 人,那么该旅游团购门票共花了多少钱?
人,那么该旅游团购门票共花了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD位于平面直角坐标系中,A、B在y轴上,且其坐标分别为A(0,a)和B(0,-b),D点坐标为(-c,a),CD与x轴交于E. 其中a、b、c均为正数,且满足![]() .
.
(1)请判断△ABD的形状并说明理由.
(2)如图,将图形沿AM折叠,使D落在x轴上F点,若现有一长度为a的线段,可与线段EF、OF构成直角三角形,求a的值.
(3)若P为x轴正半轴上一点,且满足∠APB=45°,请求出P点坐标.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空:如图,![]() 于点D,
于点D,![]() 于点E,
于点E,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.

解:∵![]() ,
,![]() (已知)
(已知)
∴![]()
![]() ( )
( )
∴![]() ( )
( )
∴( )//( )( )
∴![]() ( )( )
( )( )
∵![]() ( )
( )
∴![]() ( )
( )
∴( )//( )( )
∴![]() ( )
( )
∵![]() ( )
( )
∴![]() ( )=( )(等式性质)
( )=( )(等式性质)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com