
【题目】如图,矩形ABCD位于平面直角坐标系中,A、B在y轴上,且其坐标分别为A(0,a)和B(0,-b),D点坐标为(-c,a),CD与x轴交于E. 其中a、b、c均为正数,且满足![]() .
.
(1)请判断△ABD的形状并说明理由.
(2)如图,将图形沿AM折叠,使D落在x轴上F点,若现有一长度为a的线段,可与线段EF、OF构成直角三角形,求a的值.
(3)若P为x轴正半轴上一点,且满足∠APB=45°,请求出P点坐标.



【答案】(1)△ABD为等腰直角三角形(2)![]() 或
或![]() (3)(6,0)
(3)(6,0)
【解析】
(1)根据平方、绝对值、算术平方根的非负性分别计算出a、b、c,从而可求出AB=AD,再根据矩形的性质即可判断△ABD为等腰直角三角形;
(2)根据勾股定理先计算出EF和OF的长,然后根据构成直角三角形的条件由勾股定理可计算出a;
(3)在y轴上截取OM=ON=OP,易得△MOP、△NOP与△MNP均为等腰直角三角形,设MA=x,根据等腰三角形的性质和全等三角形的判定和性质证明三角形BNQ为直角三角形,在直角三角形中运用勾股定理解出x,从而求出点P的坐标.
(1)由![]() 得
得
a-3=0,b-2=0,c-a-b=0,解得a=3,b=2,c=5,
则由题意知OA=3,OB=2,AD=5,
所以AB=OA+OB=5=AD,
由于ABCD为矩形,则AB⊥AD,所以△ABD为等腰直角三角形;
(2)由题意知,DE=OA=3,AF=AD=5
设OF=x,在△AOF中,![]() ,即
,即
![]()
解得x=4,即OF=4,EF=OE-OF=1
若长度为a的线段可与线段EF、OF构成直角三角形,则由勾股定理得
![]() 或
或![]()
解得![]() 或
或![]() ;
;
(3)如图:

在y轴上截取OM=ON=OP,易得△MOP、△NOP与△MNP均为等腰直角三角形,
设MA=x,则BN=x+1,OP=OM=x+3
将△PMA逆时针旋转90°,使PM与NP重合,A落在点Q处,
∴∠APQ=90°,
则△PNQ≌△PMA,PQ=PA,NQ=AM,
∵∠APQ=90°,∠APB=45°,
∴∠APB=∠BPQ=45°,
又∵PA=PQ,PB=PB,
∴△PBQ≌△PBA ,
∴BQ=AB=5,
∵∠PMA=∠PNQ=45°,
∴∠BNQ=∠PNB+∠PNQ=90°,
∴三角形BNQ为直角三角形,
则![]()
即![]() ,解得
,解得
x=3(x=-4舍),则OP=x+3=6
所以P点坐标为(6,0).


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】在一个口袋中有4个完全相同的小球,它们的标号分别为1,2,3,4,从中随机摸出一个小球记下标号后放回,再从中随机摸出一个小球,求两次摸出的小球的标号之和大于4的概率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,
(1)若半径为1的⊙O经过点A、B、D,且∠A=60°,求此时菱形的边长;
(2)若点P为AB上一点,把菱形ABCD沿过点P的直线a折叠,使点D落在BC边上,利用无刻度的直尺和圆规作出直线a.(保留作图痕迹,不必说明作法和理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图
(1)若∠2=∠3,则 ∥ ,理由是 .
(2)若∠3=∠4,则 ∥ ,理由是 .
(3)若m∥n,则∠1与∠4的关系是 ,理由是 .
(4)若∠1+∠2=180°,则 ∥ ,理由是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校期末考试要给学生印制复习资料若干份,印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费用外,甲种方式还收取制版费,而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:
(1)填空:甲种收费方式的函数关系式是 , 乙种收费方式的函数关系式是 .
(2)若需印刷100﹣400份(含100和400)份复习资料,选择哪种印刷方式比较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
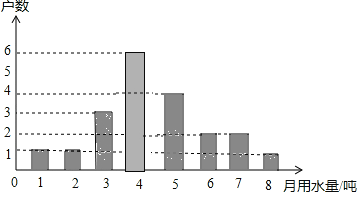
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数;
(3)若该小区有800户居民,请你估计这个小区3月份的总用水量是多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com