
【题目】某学校期末考试要给学生印制复习资料若干份,印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费用外,甲种方式还收取制版费,而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:
(1)填空:甲种收费方式的函数关系式是 , 乙种收费方式的函数关系式是 .
(2)若需印刷100﹣400份(含100和400)份复习资料,选择哪种印刷方式比较合算.
【答案】
(1)y1=0.1x+16(x≥0),y2=0.2x(x≥0)
(2)当100≤x<160时,选择乙种收费方式比较合算;
当x=160时,选择甲、乙两种收费方式都可以;
当160<x≤400时,选择甲种收费方式比较合算.
【解析】解:(1)设甲种收费的函数关系式y1=kx+b,乙种收费的函数关系式是y2=k1x,由题意,得
![]() , 20=100k1,
, 20=100k1,
解得: ![]() , k1=0.2,
, k1=0.2,
∴y1=0.1x+16(x≥0),y2=0.2x(x≥0);
所以答案是:y1=0.1x+16(x≥0),y2=0.2x(x≥0);
解:(2)由0.1x+16>0.2x,得x<160,
由0.1x+16=0.2x,得x=160,
由0.1x+16<0.2x,得x>160,
由此可知:当100≤x<160时,选择乙种收费方式比较合算;
当x=160时,选择甲、乙两种收费方式都可以;
当160<x≤400时,选择甲种收费方式比较合算.
【考点精析】本题主要考查了一元一次不等式的解法和函数自变量的取值范围的相关知识点,需要掌握步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题);使函数有意义的自变量的取值的全体,叫做自变量的取值范围才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOD.
(1)若∠AOC=32°,求∠EOF的度数;
(2)若∠EOF=60°,求∠AOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法: ① ![]() ;②数轴上的点与实数成一一对应关系;③两条直线被第三条直线所截,同位角相等;④垂直于同一条直线的两条直线互相平行;⑤两个无理数的和还是无理数;⑥无理数都是无限小数,其中正确的个数有 ___________
;②数轴上的点与实数成一一对应关系;③两条直线被第三条直线所截,同位角相等;④垂直于同一条直线的两条直线互相平行;⑤两个无理数的和还是无理数;⑥无理数都是无限小数,其中正确的个数有 ___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD位于平面直角坐标系中,A、B在y轴上,且其坐标分别为A(0,a)和B(0,-b),D点坐标为(-c,a),CD与x轴交于E. 其中a、b、c均为正数,且满足![]() .
.
(1)请判断△ABD的形状并说明理由.
(2)如图,将图形沿AM折叠,使D落在x轴上F点,若现有一长度为a的线段,可与线段EF、OF构成直角三角形,求a的值.
(3)若P为x轴正半轴上一点,且满足∠APB=45°,请求出P点坐标.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空:如图,![]() 于点D,
于点D,![]() 于点E,
于点E,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.

解:∵![]() ,
,![]() (已知)
(已知)
∴![]()
![]() ( )
( )
∴![]() ( )
( )
∴( )//( )( )
∴![]() ( )( )
( )( )
∵![]() ( )
( )
∴![]() ( )
( )
∴( )//( )( )
∴![]() ( )
( )
∵![]() ( )
( )
∴![]() ( )=( )(等式性质)
( )=( )(等式性质)
查看答案和解析>>
科目:初中数学 来源: 题型:
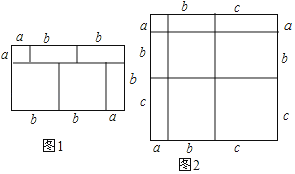
【题目】对于一个平面图形,通过两种不同的方法计算它的面积,可以得到一个关于整式乘法的等式.例如:计算左图的面积可以得到等式(a+b)(a+2b)=a2+3ab+2b2.
请解答下列问题:
(1)观察如图,写出所表示的等式: = ;
(2)已知上述等式中的三个字母a,b,c可取任意实数,若a=7x﹣5,b=﹣4x+2,c=﹣3x+4,且a2+b2+c2=37,请利用(1)所得的结论求ab+bc+ac的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,连接DE,BF,BD.
(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:如图:
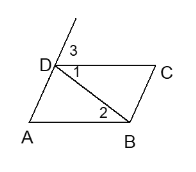
①若∠1=∠2,则 ∥ ( )
若∠DAB+∠ABC=180°,则 ∥ ( )
②当 ∥ 时,∠ C+∠ABC=180°( )
当 ∥ 时,∠3=∠C ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com