
【题目】推理填空:如图:
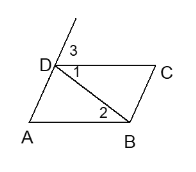
①若∠1=∠2,则 ∥ ( )
若∠DAB+∠ABC=180°,则 ∥ ( )
②当 ∥ 时,∠ C+∠ABC=180°( )
当 ∥ 时,∠3=∠C ( )
【答案】见解析
【解析】
①利用平行线的性质及判定,即先利用内错角相等,两直线平行得出AB∥CD,然后再根据同旁内角互补,两直线平行得出AD∥BC.②根据两直线平行,同旁内角互补求得两角互补.再根据两直线平行,内错角相等求得∠3=∠C.
解:①若∠1=∠2,则AB∥CD(内错角相等,两直线平行);
若∠DAB+∠ABC=180°,则AD∥BC(同旁内角互补,两直线平行);
②当AB∥CD时,∠C+∠ABC=180°(两直线平行,同旁内角互补);
当AD∥BC时,∠3=∠C(两直线平行,内错角相等).
故答案为:AB∥CD;内错角相等,两直线平行;AD∥BC;同旁内角互补,两直线平行;AB∥CD;两直线平行,同旁内角互补;AD∥BC;两直线平行,内错角相等.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】某学校期末考试要给学生印制复习资料若干份,印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费用外,甲种方式还收取制版费,而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:
(1)填空:甲种收费方式的函数关系式是 , 乙种收费方式的函数关系式是 .
(2)若需印刷100﹣400份(含100和400)份复习资料,选择哪种印刷方式比较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明把一副三角板按如图所示叠放在一起,固定三角板![]() ,将另一块三角板
,将另一块三角板![]() 绕公共顶点
绕公共顶点![]() 顺时针旋转(旋转的角度为锐角).若两块三角板有一边平行,则三角板
顺时针旋转(旋转的角度为锐角).若两块三角板有一边平行,则三角板![]() 旋转的度数可能是______.
旋转的度数可能是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
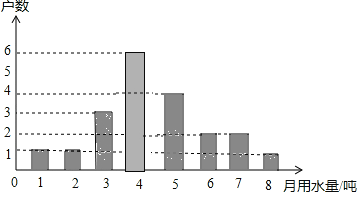
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数;
(3)若该小区有800户居民,请你估计这个小区3月份的总用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
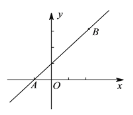
【题目】如图,已知直线y1经过点A(-1,0)与点B(2.3),另一条直线y2经过点B,且与x轴交于点P(m.0).
(1)求直线y1的解析式;
(2)若三角形ABP的面积为![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的方格纸中,![]() 的顶点都在方格纸格点上.
的顶点都在方格纸格点上.

(1)将![]() 经过平移后得到
经过平移后得到![]() ,图中标出了点A的对应点D,补全
,图中标出了点A的对应点D,补全![]() ;
;
(2)在图中画出![]() 的中线BG和高CH;
的中线BG和高CH;
(3)在(1)条件下,AD与CF的关系是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益z(元)会相应降低且z与x之间也大致满足如图②所示的一次函数关系.
(1)在政府未出台补贴措施前,该商场销售彩电的总收益额为多少元?
(2)在政府补贴政策实施后,分别求出该商场销售彩电台数y和每台家电的收益z与政府补贴款额x之间的函数关系式;
(3)要使该商场销售彩电的总收益w(元)最大,政府应将每台补贴款额x定为多少并求出总收益w的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l1:y=﹣![]() x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.
x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.
(1)求A,B两点的坐标;
(2)求△BOC的面积;
(3)如图2,若有一条垂直于x轴的直线l以每秒1个单位的速度从点A出发沿射线AO方向作匀速滑动,分别交直线l1,l2及x轴于点M,N和Q.设运动时间为t(s),连接CQ.
①当OA=3MN时,求t的值;
②试探究在坐标平面内是否存在点P,使得以O、Q、C、P为顶点的四边形构成菱形?若存在,请直接写出t的值;若不存在,请说明理由.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com