
【题目】为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益z(元)会相应降低且z与x之间也大致满足如图②所示的一次函数关系.
(1)在政府未出台补贴措施前,该商场销售彩电的总收益额为多少元?
(2)在政府补贴政策实施后,分别求出该商场销售彩电台数y和每台家电的收益z与政府补贴款额x之间的函数关系式;
(3)要使该商场销售彩电的总收益w(元)最大,政府应将每台补贴款额x定为多少并求出总收益w的最大值.
【答案】
(1)解:该商场销售家电的总收益为
800×200=160000(元)
(2)解:根据题意设
y=k1x+800,Z=k2x+200
∴400k1+800=1200,200k2+200=160
解得k1=1,k2=﹣ ![]()
∴y=x+800,Z=﹣ ![]() x+200
x+200
(3)解:W=yZ=(x+800)(﹣ ![]() x+200)=﹣
x+200)=﹣ ![]() x2+40x+160000
x2+40x+160000
=﹣ ![]() (x﹣100)2+162000.
(x﹣100)2+162000.
∵﹣ ![]() <0,
<0,
∴W有最大值.
当x=100时,W最大=162000
∴政府应将每台补贴款额x定为100元,总收益有最大值
其最大值为162000元.
【解析】(1)找出图像与纵轴的交点,透彻理解其含义,收益=每台收益![]() 销量;(2)由图像可求出每条直线上两点坐标,利用待定系数法求出解析式即可;(3)根据“收益=每台收益
销量;(2)由图像可求出每条直线上两点坐标,利用待定系数法求出解析式即可;(3)根据“收益=每台收益![]() 销量”可得出W=yZ=(x+800)(﹣
销量”可得出W=yZ=(x+800)(﹣ ![]() x+200)化为顶点式,求出最值.
x+200)化为顶点式,求出最值.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
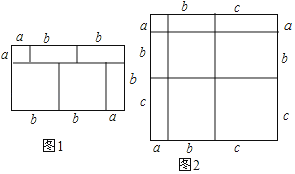
【题目】对于一个平面图形,通过两种不同的方法计算它的面积,可以得到一个关于整式乘法的等式.例如:计算左图的面积可以得到等式(a+b)(a+2b)=a2+3ab+2b2.
请解答下列问题:
(1)观察如图,写出所表示的等式: = ;
(2)已知上述等式中的三个字母a,b,c可取任意实数,若a=7x﹣5,b=﹣4x+2,c=﹣3x+4,且a2+b2+c2=37,请利用(1)所得的结论求ab+bc+ac的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,那么关于此二次函数的下列四个结论:①a+b+c<0;②c>1;③b2﹣4ac>0;④2a﹣b<0,其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:如图:
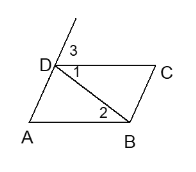
①若∠1=∠2,则 ∥ ( )
若∠DAB+∠ABC=180°,则 ∥ ( )
②当 ∥ 时,∠ C+∠ABC=180°( )
当 ∥ 时,∠3=∠C ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③垂直于同一直线的两条直线互相平行;④平行于同一直线的两条直线互相平行;⑤两条直线被第三条直线所截,如果同旁内角相等,那么这两条直线互相平行;⑥连结![]() 、
、![]() 两点的线段就是
两点的线段就是![]() 、
、![]() 两点之间的距离,其中正确的有( )
两点之间的距离,其中正确的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海域有A,B,C三艘船正在捕鱼作业,C船突然出现故障,向A,B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.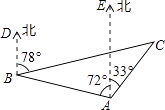
(1)求∠ABC的度数;
(2)A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 O 在直线 AB 上,OC⊥OD,∠EDO 与∠1 互余.
(1)求证:ED//AB;
(2)OF 平分∠COD 交 DE 于点 F,若OFD=70,补全图形,并求∠1 的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com