
【题目】二次函数y=ax2+bx+c的图象如图所示,那么关于此二次函数的下列四个结论:①a+b+c<0;②c>1;③b2﹣4ac>0;④2a﹣b<0,其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】①与图象知,当x=1时,y<0,即a+b+c<0.故此选项正确;
②∵图象与y轴交点坐标在y轴上方,但在1的下方,
∴1>c>0,故此选项错误;
③图象与x轴有2个交点,依据根的判别式可知b2﹣4ac>0,故此选项正确;
④∵对称轴方程﹣1<﹣ ![]() <0,
<0,
∴1> ![]() >0;
>0;
∵a<0,
∴b>2a,
∴2a﹣b<0.故此选项正确;
综上所述,正确的说法有①、③、④,共有3个.
所以答案是:C.
【考点精析】掌握二次函数的性质和二次函数图象以及系数a、b、c的关系是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


科目:初中数学 来源: 题型:
【题目】如图
(1)若∠2=∠3,则 ∥ ,理由是 .
(2)若∠3=∠4,则 ∥ ,理由是 .
(3)若m∥n,则∠1与∠4的关系是 ,理由是 .
(4)若∠1+∠2=180°,则 ∥ ,理由是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明把一副三角板按如图所示叠放在一起,固定三角板![]() ,将另一块三角板
,将另一块三角板![]() 绕公共顶点
绕公共顶点![]() 顺时针旋转(旋转的角度为锐角).若两块三角板有一边平行,则三角板
顺时针旋转(旋转的角度为锐角).若两块三角板有一边平行,则三角板![]() 旋转的度数可能是______.
旋转的度数可能是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
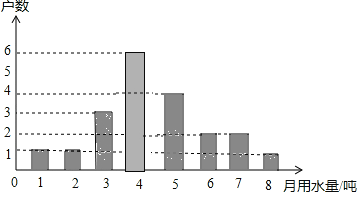
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数;
(3)若该小区有800户居民,请你估计这个小区3月份的总用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
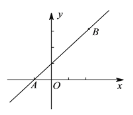
【题目】如图,已知直线y1经过点A(-1,0)与点B(2.3),另一条直线y2经过点B,且与x轴交于点P(m.0).
(1)求直线y1的解析式;
(2)若三角形ABP的面积为![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益z(元)会相应降低且z与x之间也大致满足如图②所示的一次函数关系.
(1)在政府未出台补贴措施前,该商场销售彩电的总收益额为多少元?
(2)在政府补贴政策实施后,分别求出该商场销售彩电台数y和每台家电的收益z与政府补贴款额x之间的函数关系式;
(3)要使该商场销售彩电的总收益w(元)最大,政府应将每台补贴款额x定为多少并求出总收益w的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC于点G,
求证:(1)DF∥BC;
(2)FG=FE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com