
【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点F.
求证:BF=AC.
【答案】证明:∵CD⊥AB,
∴∠BDC=∠CDA=90°;
∵∠ABC=45°,
∴∠DCB=∠ABC=45°(三角形的内角和定理),
∴DB=DC(等角对等边);
∵BE⊥AC,
∴∠AEB=90°,
∴∠A+∠ABE=90°(直角三角形的两个锐角互为余角);
∵∠CDA=90°,
∴∠A+∠ACD=90°,
∴∠ABE=∠ACD(同角的余角相等);
在△BDF和△CDA中,
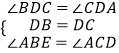 ,
,
∴△BDF≌△CDA(ASA),
∴BF=AC(全等三角形的对应边相等).
【解析】要证BF=AC,就需要证明△BDF和△CDA全等,由已知条件可知它们是直角三角形。抓住题中关键的已知条件∠ABC=45°,CD⊥AB于D,可得到△BDC是等腰直角三角形,得出DB=DC。再根据同角的余角相等或等角的余角相等,可得到两三角形的另一组对应角相等,即可证得结论。
【考点精析】认真审题,首先需要了解余角和补角的特征(互余、互补是指两个角的数量关系,与两个角的位置无关).


科目:初中数学 来源: 题型:
【题目】若二次函数 y=ax2+bx+c(a<0) 的图象经过点(2,0),且其对称轴为直线 x=1 ,则使函数值 y>0 成立的 x 的取值范围是( )
A.![]() x<4 或 x>2
x<4 或 x>2
B.![]() 4 ≤ x ≤ 2
4 ≤ x ≤ 2
C.![]() x ≤ 4 或 x ≥ 2
x ≤ 4 或 x ≥ 2
D.![]() 4<x<2
4<x<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,王老师拿出一张如图 1 所示的长方形![]() 纸(对边
纸(对边![]() ,四个角都是直角), 要求同学们用直尺和量角器在 AB 边上找一点 E,使
,四个角都是直角), 要求同学们用直尺和量角器在 AB 边上找一点 E,使![]() .
.

(1)甲同学的做法:在![]() 边上任取一点
边上任取一点![]() ,以
,以![]() 为顶点,以
为顶点,以![]() 为一边,用量角器作
为一边,用量角器作![]() 角,使另外一边经过点 C,则
角,使另外一边经过点 C,则![]() 即为所求.
即为所求.
(2)乙同学的做法:以![]() 为始边,在长方形的内部,利用量角器作
为始边,在长方形的内部,利用量角器作![]() ,射线
,射线![]() 与
与![]() 交于点
交于点![]() ,则如图 2 所示
,则如图 2 所示![]() 即为所求.
即为所求.
你支持_______同学的做法,作图依据是__________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图
(1)若∠2=∠3,则 ∥ ,理由是 .
(2)若∠3=∠4,则 ∥ ,理由是 .
(3)若m∥n,则∠1与∠4的关系是 ,理由是 .
(4)若∠1+∠2=180°,则 ∥ ,理由是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC和Rt△ADE中,∠BAC=90°,∠DAE=90°,AB=AC,AD=AE,CE与BD相交于点M,BD与AC交于点N,试猜想BD与CE有何关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校期末考试要给学生印制复习资料若干份,印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费用外,甲种方式还收取制版费,而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:
(1)填空:甲种收费方式的函数关系式是 , 乙种收费方式的函数关系式是 .
(2)若需印刷100﹣400份(含100和400)份复习资料,选择哪种印刷方式比较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商人制成了一个如图所示的转盘,取名为“开心大转盘”,游戏规定:参与者自由转动转盘,转盘停止后,若指针指向字母“A”,则收费2元,若指针指向字母“B”,则奖励3元;若指针指向字母“C”,则奖励1元.一天,前来寻开心的人转动转盘80次,你认为该商人是盈利的可能性大还是亏损的可能性大?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
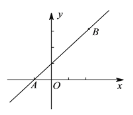
【题目】如图,已知直线y1经过点A(-1,0)与点B(2.3),另一条直线y2经过点B,且与x轴交于点P(m.0).
(1)求直线y1的解析式;
(2)若三角形ABP的面积为![]() ,求m的值.
,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com