
【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.
【答案】
(1)解:把A(﹣1,0)、B(3,0)分别代入y=x2+bx+c中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的解析式为y=x2﹣2x﹣3.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点坐标为(1,﹣4)
(2)解:由图可得当0<x<3时,﹣4≤y<0
(3)解:∵A(﹣1,0)、B(3,0),
∴AB=4.
设P(x,y),则S△PAB= ![]() AB|y|=2|y|=10,
AB|y|=2|y|=10,
∴|y|=5,
∴y=±5.
①当y=5时,x2﹣2x﹣3=5,解得:x1=﹣2,x2=4,
此时P点坐标为(﹣2,5)或(4,5);
②当y=﹣5时,x2﹣2x﹣3=﹣5,方程无解;
综上所述,P点坐标为(﹣2,5)或(4,5).
【解析】(1)方法1:将A、B两点坐标代入函数解析式建立二元一次方程组求出b、c的值,方法2:因为A(﹣1,0)、B(3,0)所以可设函数解析式为y=a(x-3)(x+1),由a=1,可求出函数解析式,再利用配方法或代入顶点坐标就可以求出抛物线的顶点坐标;(2)结合图像以及点A、B的坐标即可得出结论;(3)设点P(x,y),根据三角形的面积公式以及S△PAB=10,即可求出y的值,将y=±5分别代入函数解析式就可以求出点P的坐标。


科目:初中数学 来源: 题型:
【题目】兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上有点![]() ,
,![]() ,
,![]() ,它们表示的数分别为
,它们表示的数分别为![]() ,
,![]() ,
,![]() ,且满足:
,且满足:![]() ;
;![]() ,
,![]() ,
,![]() 三点同时出发沿数轴向右运动,它们的速度分别为:
三点同时出发沿数轴向右运动,它们的速度分别为:![]() (单位/秒),
(单位/秒),![]() (单位/秒),
(单位/秒),![]() (单位/秒).
(单位/秒).
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)运动时间![]() 等于多少时,
等于多少时,![]() 点与
点与![]() 点、
点、![]() 点的距离相等?
点的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明把一副三角板按如图所示叠放在一起,固定三角板![]() ,将另一块三角板
,将另一块三角板![]() 绕公共顶点
绕公共顶点![]() 顺时针旋转(旋转的角度为锐角).若两块三角板有一边平行,则三角板
顺时针旋转(旋转的角度为锐角).若两块三角板有一边平行,则三角板![]() 旋转的度数可能是______.
旋转的度数可能是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
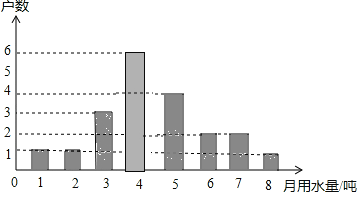
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数;
(3)若该小区有800户居民,请你估计这个小区3月份的总用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的方格纸中,![]() 的顶点都在方格纸格点上.
的顶点都在方格纸格点上.

(1)将![]() 经过平移后得到
经过平移后得到![]() ,图中标出了点A的对应点D,补全
,图中标出了点A的对应点D,补全![]() ;
;
(2)在图中画出![]() 的中线BG和高CH;
的中线BG和高CH;
(3)在(1)条件下,AD与CF的关系是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老李上周五以收盘价每股8元买入某公司股票10000股,下表为本周内每日该股票的涨跌情况(单位:元):
星期 | 一 | 二 | 三 | 四 | 五 |
股票涨跌 | -0.1 | 0.35 | -0.15 | -0.4 | 0.5 |
(1)星期三的收盘价比老李的买入价涨或跌了多少元?
(2)本周内该股票的最高收盘价出现在星期几?是多少元?
(3)已知老李买进股票时要付成交额1‰的手续费,卖出时还需要付成交额的1‰的印花税和1‰的手续费.如果老李在星期五收盘前将该股票全部卖出,则他的收益情况如何?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com