

分析 逆向思维:由知识链接可知若△ABC的某边所对的∠D与△ABC该边所对的内角 相等或互补.
迁移应用:(1)如图③中,作△ABC的外接圆交CD于E1,交AD于E2,点E1、E2即为所求.
(2)只要证明∠AEC=∠ADC,即可推出点D在△AEC的外接圆上.
(3)分两种情形讨论①作△ABC的外接圆⊙O′与对称轴交于点P,此时∠BPC=∠BAC满足条件.②把△ABC沿BC翻折得到△A′BC,设△A′BC的外接圆的圆心为O″,⊙O″交对称轴由P′,则∠BP′C=∠A′=∠BAC.分别求解即可.
解答 逆向思维:解:由知识链接可知若△ABC的某边所对的∠D与△ABC该边所对的内角 相等或互补,
则点D在该三角形的外接圆上.
故答案为相等或互补.
迁移应用:(1)解:如图③中,作△ABC的外接圆交CD于E1,交AD于E2,点E1、E2即为所求.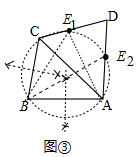
(2)证明:如图④中,设AD与EC交于点O.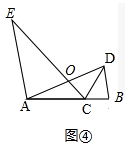
∵AD=AB,
∴∠ADB=∠B,
∵AE∥BD,
∴∠EAD=∠ADB,
∴∠EAD=∠B,
∵∠ECA=∠CDB,
∠ACD=∠ECA+∠ECD=∠B+∠CDB,
∴∠ECD=∠B,
∴∠EAD=∠ECD,
∵∠EOA=∠DOC,
∴∠AEC=∠ADC,
∴点D在△AEC的外接圆上.
(3)解:如图⑤中,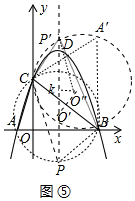
①作△ABC的外接圆⊙O′与对称轴交于点P,此时∠BPC=∠BAC满足条件.
∵C(0,4a),B(4,0),
∴直线BC的解析式为y=-ax+4a,线段BC的中垂线的解析式为y=$\frac{1}{a}$x+2a-$\frac{2}{a}$,
∴O′($\frac{3}{2}$,2a-$\frac{1}{2a}$),△ABC的外接圆的半径=$\sqrt{\frac{25}{4}+(2a-\frac{1}{2a})^{2}}$,
∴P[$\frac{3}{2}$,$\sqrt{\frac{25}{4}+(2a-\frac{1}{2a})^{2}}$-2a+$\frac{1}{2a}$].
②把△ABC沿BC翻折得到△A′BC,设△A′BC的外接圆的圆心为O″,⊙O″交对称轴由P′,则∠BP′C=∠A′=∠BAC,点O′与O″关于直线BC对称,
易知O″($\frac{5}{2}$,2a+$\frac{1}{2a}$),作O″K⊥对称轴于K,
在Rt△P′O″K中,P′K=$\sqrt{\frac{25}{4}+(2a-\frac{1}{2a})^{2}-1}$=$\sqrt{\frac{21}{4}+(2a-\frac{1}{2a})^{2}}$,
∴P′[$\frac{3}{2}$,2a+$\frac{1}{2a}$+$\sqrt{\frac{21}{4}+(2a-\frac{1}{2a})^{2}}$].
综上所述,满足条件的点P坐标为P[$\frac{3}{2}$,$\sqrt{\frac{25}{4}+(2a-\frac{1}{2a})^{2}}$-2a+$\frac{1}{2a}$]或[$\frac{3}{2}$,2a+$\frac{1}{2a}$+$\sqrt{\frac{21}{4}+(2a-\frac{1}{2a})^{2}}$].
点评 本题考查了二次函数的相关性质、一次函数的相关性质、圆周角定理、轴对称图形的性质、勾股定理等知识点.本题解题技巧要求高,因此对考生的综合能力提出了很高的要求,以BC为对称轴构造△A′BC是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com