
【题目】探究:如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,直线l3有一点P,
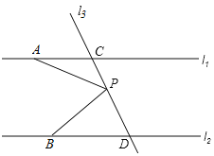
(1)若点P在C、D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化,并说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?并说明理由.
【答案】(1)∠APB=∠PAC+∠PBD,理由见解析;(2)当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB;当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.理由见解析.
【解析】
试题分析:(1)过点P作PE∥l1根据l1∥l2得出PE∥l2∥l1,从而得出∠PAC=∠1,∠PBD=∠2,然后得出答案;(2)分点P在C、D两点的外侧运动,在l1上方和在l2下方时两种情况,分别根据(1)的方法得出答案.
试题解析:(1)当点P在C、D之间运动时,∠APB=∠PAC+∠PBD.理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)ⅰ)当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
ⅱ)当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.理由如下:
∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
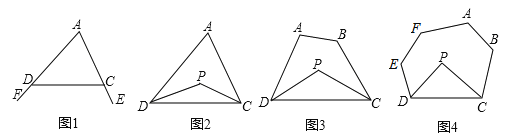
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
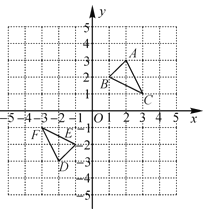
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a,b的值.
(3)求图中△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A+∠B=∠C;②∠A﹕∠B﹕∠C=1﹕2﹕3;③∠A=![]() ∠B=
∠B=![]() ∠C;④∠A=∠B=2∠C;⑤∠A=∠B=
∠C;④∠A=∠B=2∠C;⑤∠A=∠B=![]() ∠C,能确定△ABC为直角三角形的条件有( )
∠C,能确定△ABC为直角三角形的条件有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com