
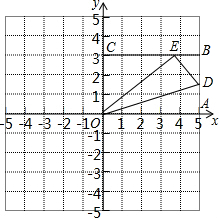
 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,B(5,3)在AB边上取一点F,将纸片沿OD翻折,使点A落在BC边上的点E处,求点D,E的坐标.
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,B(5,3)在AB边上取一点F,将纸片沿OD翻折,使点A落在BC边上的点E处,求点D,E的坐标. 分析 根据折叠的性质可得出OE=OA,可在RT△OCE中,用勾股定理求出CE的长,也就求出了E点的坐标,由△CEO∽△BDE,列方程$\frac{CE}{BD}=\frac{OC}{BE}$,即$\frac{4}{BD}=\frac{3}{1}$,求得BD=$\frac{4}{3}$,于是得到结果.
解答 解:∵四边形OABC是矩形,
∴BC=OA,OC=AB,
∵B(5,3),
∴BC=OA=5,OC=AB=3,
∵在AB边上取一点F,将纸片沿OD翻折,使点A落在BC边上的点E处,
∴OE=OA=5,OC=AB=3,
∴CE=$\sqrt{O{E}^{2}-O{C}^{2}}$=4,
∴E(4,3),
∴BE=1,
∵∠DEO=90°,
∴∠DEB+∠BDE=∠BED+∠CEO=90°,
∴∠BDE=∠CEO,
∴△CEO∽△BDE,
∴$\frac{CE}{BD}=\frac{OC}{BE}$,即$\frac{4}{BD}=\frac{3}{1}$,
∴BD=$\frac{4}{3}$,
∴AD=$\frac{5}{3}$,
∴D(5,$\frac{5}{3}$).
点评 本题主要考查了翻折变换的性质以及勾股定理,现实世界的判定和性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com