
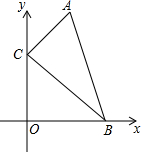
 如图,在直角坐标系中,点A、B的坐标分别为(2,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.
如图,在直角坐标系中,点A、B的坐标分别为(2,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.
|
|
 ,
,
|
|
| 4 |
| 5 |
| 12 |
| 5 |
| 12 |
| 5 |
| 12 |
| 5 |
 ,
,| 11 |
| 8 |
| 11 |
| 8 |


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
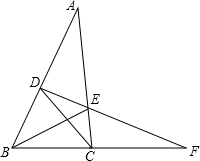 如图,在△ABC,点D、E分别在AB、AC上,连结DE并延长交BC的延长线于点F,连结DC、BE,若∠BDE+∠BCE=180°.请写出图中的两对相似三角形(不另外添加字母和线),并选择其中的一对进行证明.
如图,在△ABC,点D、E分别在AB、AC上,连结DE并延长交BC的延长线于点F,连结DC、BE,若∠BDE+∠BCE=180°.请写出图中的两对相似三角形(不另外添加字母和线),并选择其中的一对进行证明.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、平均数为10,方差是2 |
| B、平均数是11,方差为3 |
| C、平均数为11,方差为2 |
| D、平均数为12,方差为4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 用反正法证明命题“如图,如果AB∥CD,AB∥EF,那么CD∥EF”时,证明的第一个步骤是( )
用反正法证明命题“如图,如果AB∥CD,AB∥EF,那么CD∥EF”时,证明的第一个步骤是( )| A、假设AB不平行于CD |
| B、假设AB不平行于EF |
| C、假设CD∥EF |
| D、假设CD不平行于EF |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com