
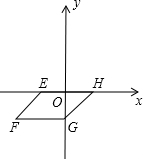
 已知:如图,在?EFGH中,点F的坐标是(-2,-1),∠EFG=45°.
已知:如图,在?EFGH中,点F的坐标是(-2,-1),∠EFG=45°.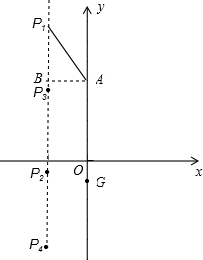

 )或P2(-2,3-
)或P2(-2,3- )
) )或P4(-2,-1-
)或P4(-2,-1- )
) )
) )或(-2,-1+
)或(-2,-1+ )或(-2,-1-
)或(-2,-1- ).
).

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
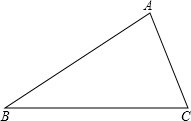 已知:如图,在△ABC中,AB=3,AC=2,能否在AC上(不同于A,C)找到点D,过点D作DE∥AB交于BC于E,过点E作EF∥AC交AB于F,连接FD,将△ABC分割成四个相似的小三角形,但其中至少有两个小三角形的相似比不等于1?若能,求出点D位置;若不能,请说明理由.
已知:如图,在△ABC中,AB=3,AC=2,能否在AC上(不同于A,C)找到点D,过点D作DE∥AB交于BC于E,过点E作EF∥AC交AB于F,连接FD,将△ABC分割成四个相似的小三角形,但其中至少有两个小三角形的相似比不等于1?若能,求出点D位置;若不能,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 D分别交AB,CD于点E,F.
D分别交AB,CD于点E,F.| OA |
| OC |
| OD |
| OB |
| OE |
| AD |
| OF |
| BC |
查看答案和解析>>
科目:初中数学 来源: 题型:
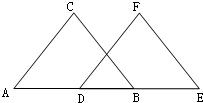 20、看图填空:
20、看图填空:查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)在△ABC中,AB=m2-n2,AC=2mn,BCm2+n2=(m>n>0).
(1)在△ABC中,AB=m2-n2,AC=2mn,BCm2+n2=(m>n>0).| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,在△ABC中,D是BC边的中点,E是AD的中点,连接BE并延长到点F,使EF=BE,连接AF、CF.
已知:如图,在△ABC中,D是BC边的中点,E是AD的中点,连接BE并延长到点F,使EF=BE,连接AF、CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com