
 如图是二次函数y=ax2+bx+c的图象,下列结论:
如图是二次函数y=ax2+bx+c的图象,下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据抛物线的顶点坐标确定二次三项式ax2+bx+c的最大值;
②根据x=2时,y<0确定4a+2b+c的符号;
③根据抛物线的对称性确定一元二次方程ax2+bx+c=1的两根之和;
④根据函数图象确定使y≤3成立的x的取值范围.
解答 解:∵抛物线的顶点坐标为(-1,4),∴二次三项式ax2+bx+c的最大值为4,①正确;
∵x=2时,y<0,∴4a+2b+c<0,②正确;
根据抛物线的对称性可知,一元二次方程ax2+bx+c=1的两根之和为-2,③错误;
使y≤3成立的x的取值范围是x≥0或x≤-2,④错误,
故选:B.
点评 本题考查的是二次函数的图象、二次函数的最值、二次函数与不等式,掌握二次函数的性质、正确获取图象信息是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
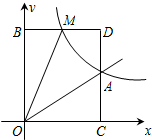 已知反比例函数$y=\frac{k}{x}$的图象经过点A(2,1).点M(m,n)(0<m<2)是该函数图象上的一动点,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
已知反比例函数$y=\frac{k}{x}$的图象经过点A(2,1).点M(m,n)(0<m<2)是该函数图象上的一动点,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 水平放置的容器内原有210毫米高的水,如图,将若干个球逐一放入该容器中,每放入一个大球水面就上升4毫米,每放入一个小球水面就上升3毫米,假定放入容器中的所有球完全浸没水中且水不溢出.设水面高为y毫米.
水平放置的容器内原有210毫米高的水,如图,将若干个球逐一放入该容器中,每放入一个大球水面就上升4毫米,每放入一个小球水面就上升3毫米,假定放入容器中的所有球完全浸没水中且水不溢出.设水面高为y毫米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
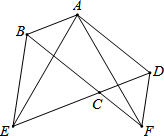 如图,在?ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.
如图,在?ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为( )| A. | 26° | B. | 36° | C. | 46° | D. | 56° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$x+3>0 | B. | $\frac{1}{2}$x+3<0 | C. | $\frac{1}{2}$(x+3)>0 | D. | $\frac{1}{2}$(x+3)<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com