
【题目】如图,AD是直角△ABC (∠C=90°)的角平分线,EF⊥AD于D , 与AB及AC的延长线分别交于E , F , 写出图中的一对全等三角形是 ;一对相似三角形是 . 
【答案】△AED和△AFD;△AED和△DFC
【解析】∵AD是∠BAC的角平分线,∴∠DAE=∠DAF ,
在△AED和△AFD中, ![]() DAE=
DAE= ![]() DAF,AD=AD,
DAF,AD=AD, ![]() ADE=
ADE= ![]() ADF=
ADF= ![]() ,
,
∴△AED≌△AFD(ASA),
∴∠AED=∠DFC ,
∵∠FDC+∠CDA=90°,∠CDA+∠CAD=90°,∠DAC=∠DAE ,
∴∠FDC=∠DAE ,
∴△AED∽△DFC(AA),
所以答案是△AED≌△AFD、△AED∽△DFC .
【考点精析】利用相似三角形的判定对题目进行判断即可得到答案,需要熟知相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】某公司有甲种原料260kg,乙种原料270kg,计划用这两种原料生产A、B两种产品共40件.生产每件A种产品需甲种原料8kg,乙种原料5kg,可获利润900元;生产每件B种产品需甲种原料4kg,乙种原料9kg,可获利润1100元.设安排生产A种产品x件.
(1)完成下表
甲(kg) | 乙(kg) | 件数(件) | |
A | 5x | x | |
B | 4(40﹣x) | 40﹣x |
(2)安排生产A、B两种产品的件数有几种方案?试说明理由;
(3)设生产这批40件产品共可获利润y元,将y表示为x的函数,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC>AC , 点D在BC上,且DC=AC , ∠ACB的平分线CF交AD于F , 点E是AB的中点,连接EF . 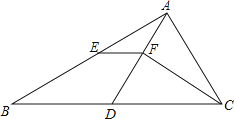
(1)求证:2EF=BD ,
(2)四边形BDFE的面积为6,求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件,不能判定△ABC与△DEF相似的是( )
A.∠C=∠F=90°,∠A=55°,∠D=35°
B.∠C=∠F=90°,AB=10,BC=6,DE=15,EF=9
C.∠C=∠F=90°, ![]() =
= ![]()
D.∠B=∠E=90°, ![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.若设小道的宽为x米,则可列方程为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8:00~12:00,下午14:00~18:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于45件.
生产产品件数与所用时间之间的关系见下表:
生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(分) |
10 | 10 | 500 |
15 | 20 | 900 |
信息三:按件计酬,每生产一件甲产品可得6元,每生产一件乙产品可得10元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A的坐标为(1,0),P是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).
(1)点( ![]() ,
, ![]() )的“双角坐标”为;
)的“双角坐标”为;
(2)若点P到x轴的距离为 ![]() ,则m+n的最小值为 .
,则m+n的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数 ![]() 与反比例函数
与反比例函数 ![]() 的图象在第一象限的交点为A(1,n).
的图象在第一象限的交点为A(1,n). 
(1)求m与n的值;
(2)设一次函数的图象与x轴交于点B,连结OA,求∠BAO的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com