
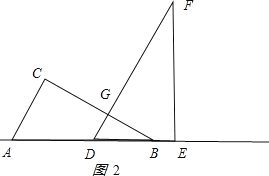
����Ŀ���������ǰ�ABC��DEF������ͼ��ʾ��λ�ðڷţ���B���D�غϣ���AB���DE��ͬһ��ֱ���ϣ�����ͼ�������еĵ㣬�߶���ͬһƽ���ڣ������У���C=��DEF=90�㣬��ABC=��F=30�㣬AC=DE=6cm���̶ֹ����ǰ�DEF�������ǰ�ABC������DE����ƽ�ƣ�����C���ڱ�EF��ʱֹͣ�˶��������ǰ�ƽ�Ƶľ���Ϊx��cm�����������ǰ��ص����ֵ����Ϊy��cm2����
��1������C���ڱ�EF��ʱ��x=��cm��
��2����y����x�ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
��3�����BC���е�Ϊ��M����DF���е�Ϊ��N��ֱ��д�������ǰ�ƽ�ƹ����У���M���N֮��������Сֵ��
���𰸡�
��1��
�⣺��ͼ1��ʾ����CG��AB��G�㣮
 ��
��
��Rt��ABC����AC=6����ABC=30����
BC=![]() =6
=6![]() ��
��
��Rt��BCG��BG=BCcos30��=9��
�ı���CGEH�Ǿ��Σ�
CH=GE=BG+BE=9+6=15cm��
�ʴ�Ϊ��15��
��2��
�⣺�ٵ�0��x��6ʱ����ͼ2��ʾ��
 ��
��
��GDB=60�㣬��GBD=30�㣬DB=x����
DG=![]() x��BG=
x��BG=![]() x���ص����ֵ����Ϊy=
x���ص����ֵ����Ϊy=![]() DGBG=
DGBG=![]() ��
��![]() x��
x��![]() x=
x=![]() x2
x2
�ڵ�6��x��12ʱ����ͼ3��ʾ��
 ��
��
BD=x��DG=![]() x��BG=
x��BG=![]() x��BE=x��6��EH=
x��BE=x��6��EH=![]() ��x��6����
��x��6����
�ص����ֵ����Ϊy=S��BDG��S��BEH=![]() DGBG��
DGBG��![]() BEEH��
BEEH��
��y=![]() ��
��![]() x��
x��![]() x��
x��![]() ��x��6��
��x��6��![]() ��x��6��
��x��6��
����y=��![]() x2+2
x2+2![]() x��6
x��6![]() ��
��
�۵�12��x��15ʱ����ͼ4��ʾ��
 ��
��
AC=6��BC=6![]() ��BD=x��BE=��x��6����EG=
��BD=x��BE=��x��6����EG=![]() ��x��6����
��x��6����
�ص����ֵ����Ϊy=S��ABC��S��BEG=![]() ACBC��
ACBC��![]() BEEG��
BEEG��
��y=![]() ��6��6
��6��6![]() ��
��![]() ��x��6��
��x��6��![]() ��x��6����
��x��6����
����y=18![]() ��
��![]() ��x2��12x+36��=��
��x2��12x+36��=��![]() x2+2
x2+2![]() x+12
x+12![]() ��
��
����������y=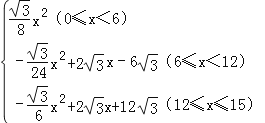 ��
��
��3��
�⣺��ͼ5��ʾ��NG��DE��G�㣮
 ��
��
��M��NG��ʱMN��̣�
NG�ǡ�DEF����λ�ߣ�
NG=![]() EF=
EF=![]() ��
��
MB=![]() CB=3
CB=3![]() ����B=30�㣬
����B=30�㣬
MG=![]() MB=
MB=![]() ��
��
MN��С=3![]() ��
��![]() =
=![]() ��
��
����������1������������Ǻ������ɵ�BG�ij��������߶εĺͲ��GE�ij������ݾ��ε����ʣ��ɵô𰸣�
��2���������ۣ��ٵ�0��t��6ʱ�����������ε������ʽ���ɵô𰸣��ڵ�6��t��12ʱ���۵�12��t��15ʱ����������ĺͲ�ɵô𰸣�
��3�����ݵ���ֱ�������е�������д��߶���̣��ɵ�M���߶�NG�ϣ����������ε���λ�ߣ��ɵ�NG�ij�������������Ǻ������ɵ�MG�ij��������߶εĺͲ�ɵô𰸣�
���⿼����ͼ�ε��ƶ��任���漰֪ʶ���о��ε����ʣ�������Ǻ����������������ʽ���д������ʣ���λ�����ʵ�.


 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=a��x��1��2��c��ͼ����ͼ��ʾ����һ�κ���y=ax+c�Ĵ���ͼ������ǣ� �� 
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ִ���λ����ͷO����������A�����ִ���λ����ͷO����������C������á�CAO=45�㣬�ִ���������������ʻ��ͬʱ�ִ�������������������ʻ�����ǵ��ٶȷֱ�Ϊ45km/h��36km/h������0.1h���ִ�����ʻ��B�����ִ�����ʻ��D������á�DBO=58�㣬��ʱB��������ͷO��Զ�����ο����ݣ�sin58���0.85��cos58���0.53��tan58���1.60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC����ABΪֱ���ġ�O��BC�ཻ�ڵ�D����CA���ӳ����ཻ�ڵ�E������D��DF��AC�ڵ�F��
��1����˵��DF�ǡ�O������
��2����AC=3AE����tanC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ҫ�Ӽס�������ͬѧ��ѡ��һ���������༶�μ������������ͼ���������10�����ѵ���ɼ�������ͳ��ͼ��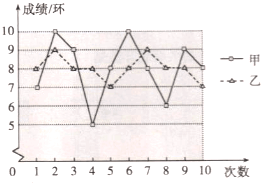
��1������ü�ƽ���ɼ�Ϊ8�������ҵ�ƽ���ɼ���
��2���۲�ͼ�Σ�ֱ��д���ף�����10������ɼ��ķ���s��2��s��2�ĸ���
��3����������༶����ѡ�ֵ�����ɼ�����7�����ң�����Ӧ��ѡ ���������ʣ���������༶����ѡ�ֵ�����ɼ�����9�����ң�����Ӧ��ѡ ���������ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ĺ����������ſ�Ƭ����Ƭ����ֱ������ĸa��b��c��ÿ�ſ�Ƭ����ĸ��ͬ����������ͬ��С���ȴӺ�����������һ�ſ�Ƭ��������ĸ��Żز����ȣ��ٴӺ�����������һ�ſ�Ƭ��������ĸ���û���״ͼ�����б����ķ�������С�����γ���Ŀ�Ƭ�ϵ���ĸ��ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һԪ���η���M��ax2+bx+c=0��N��cx2+bx+a=0������ac��0��a��c�������ĸ������У�������ǣ�������
A.�������M��������ȵ�ʵ��������ô����NҲ��������ȵ�ʵ����
B.�������M������������ͬ����ô����N����������Ҳ��ͬ
C.���5�Ƿ���M��һ��������ô![]() �Ƿ���N��һ����
�Ƿ���N��һ����
D.�������M�ͷ���N��һ����ͬ�ĸ�����ô���������x=1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У��Խ���AC��BD�ཻ�ڵ�O����CAB=��ACB������B��BE��AB��AC�ڵ�E��
��1����֤��AC��BD;
��2����AB=14��cos��CAB=![]() �����߶�OE�ij���
�����߶�OE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������ABCD�У�E��CD�ϵ�һ�㣬����BE��AC��O������DO���ӳ���BC��E��
��1����֤����FOC�ա�EOC;
��2������ͼ�е�AD��BE�ֱ��ӳ����ڵ�N����EM��BC��CN��M��������FM���õ�ͼ2��
��֤����![]() ����FD=FM��
����FD=FM��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com