
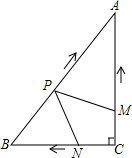
 ��ͼ����Rt��ABC�У���C=90�㣬AC=4cm��BC=3cm������M��N�ӵ�Cͬʱ����������ÿ��1cm���ٶȷֱ���CA��CB���յ�A��B�ƶ���ͬʱ����P�ӵ�B��������ÿ��2cm���ٶ���BA���յ�A�ƶ�������PM��PN���ƶ�ʱ��Ϊt����λ���룬0��t��2.5��
��ͼ����Rt��ABC�У���C=90�㣬AC=4cm��BC=3cm������M��N�ӵ�Cͬʱ����������ÿ��1cm���ٶȷֱ���CA��CB���յ�A��B�ƶ���ͬʱ����P�ӵ�B��������ÿ��2cm���ٶ���BA���յ�A�ƶ�������PM��PN���ƶ�ʱ��Ϊt����λ���룬0��t��2.5������ ��1���ȸ��ݹ��ɶ������AB�ij��������߶εĺͲ�ɵõ������
��2���������ۣ���AMP�ס�ABC�͡�APM�ס�ABC����������������������εĶ�Ӧ�߳ɱ�������t��ֵ��
��3����ͼ������P��PH��BC�ڵ�H������ƽ����PH��AC����ƽ���߷��߶γɱ��������t��ʾ��PH��ֵ��Ȼ����ݡ�S=S��ABC-S��BPH���г�S��t�Ĺ�ϵʽS=$\frac{4}{5}$��t-$\frac{3}{2}$��2+$\frac{21}{5}$��0��t��2.5�������ɶ��κ�����ֵ�����ɵõ�S����Сֵ��
��� �⣺��1������Rt��ABC�У���C=90�㣬AC=4cm��BC=3cm��
��AB=$\sqrt{{AC}^{2}+{BC}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5��
��AM=AC-CM=4-t��AP=AB-PB=5-2t��
�ʴ�Ϊ��4-t��5-2t��
��2����A��P��MΪ��������������ABC���ƣ������������
�ٵ���AMP�ס�ABCʱ��$\frac{AP}{AC}$=$\frac{AM}{AB}$����$\frac{5-2t}{4}$=$\frac{4-t}{5}$��
���t=$\frac{3}{2}$��
�ڵ���APM�ס�ABCʱ��$\frac{AM}{AC}$=$\frac{AP}{AB}$����$\frac{4-t}{4}$=$\frac{5-2t}{5}$��
���t=0���������⣬��ȥ����
������������t=$\frac{3}{2}$ʱ����A��P��MΪ��������������ABC���ƣ�
��3������ijһʱ��t��ʹ�ı���APNC�����S����Сֵ���������£�
�������ijһʱ��t��ʹ�ı���APNC�����S����Сֵ��
��ͼ������P��PH��BC�ڵ�H����PH��AC��
��$\frac{PH}{AC}$=$\frac{PB}{AB}$����$\frac{PH}{4}$=$\frac{2t}{5}$��
��PH=$\frac{8}{5}$t��
��S=S��ABC-S��BPN��
=$\frac{1}{2}$��3��4-$\frac{1}{2}$����3-t��•$\frac{8}{5}$t��
=$\frac{4}{5}$��t-$\frac{3}{2}$��2+$\frac{21}{5}$��0��t��2.5����
��$\frac{4}{5}$��0��
��S����Сֵ��
��t=$\frac{3}{2}$ʱ��S��Сֵ=$\frac{21}{5}$��
�𣺵�t=$\frac{3}{2}$ʱ���ı���APNC�����S����Сֵ������Сֵ��$\frac{21}{5}$��
���� �����ۺϿ�������������ۺ��⣬�漰�����������ε��ж������ʡ�ƽ���߷��߶γɱ��������κ�����ֵ�����Լ������������ʽ�����1����ʱ��һ��Ҫ�������ۣ��Է�©�⣮���⣬�������������εĶ�Ӧ�߳ɱ�������ʱ���������Ӧ�ߣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������OABC�ı�OA��OC���������ϣ���B������Ϊ��-4��4������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ���x�����O�˶�����Q�ӵ�Oͬʱ����������ͬ���ٶ���x����������˶����涨��P�����Oʱ����QҲֹͣ�˶�������BP����P����BP�Ĵ��ߣ������Qƽ����y���ֱ��l�ཻ�ڵ�D��BD��y�ύ�ڵ�E������PE�����P�˶���ʱ��Ϊt��s����
��ͼ��������OABC�ı�OA��OC���������ϣ���B������Ϊ��-4��4������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ���x�����O�˶�����Q�ӵ�Oͬʱ����������ͬ���ٶ���x����������˶����涨��P�����Oʱ����QҲֹͣ�˶�������BP����P����BP�Ĵ��ߣ������Qƽ����y���ֱ��l�ཻ�ڵ�D��BD��y�ύ�ڵ�E������PE�����P�˶���ʱ��Ϊt��s�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x3-5x2��-��-4x+9�� | B�� | x3-5x2-��4x+9�� | C�� | -��-x3+5x2��-��4x-9�� | D�� | x3+9-��5x2-4x�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com