
【题目】一条笔直的公路上顺次有A、B、C三地,甲、乙两车同时从B地出发,向A地均速行驶。甲车到达A地后停止,乙车到达A地后停留1小时,然后再调头按原速向C地行驶。若A、B两地相距400千米,在两车行驶过程中,甲、乙两车之间的距离![]() (千米)与乙车行驶时间
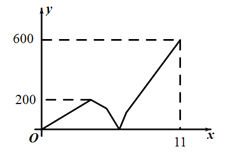
(千米)与乙车行驶时间![]() (小时)之间的函数图象如图所示,则他们出发后经过___________小时相遇.
(小时)之间的函数图象如图所示,则他们出发后经过___________小时相遇.
【答案】6
【解析】
观察函数图象可知A、C两地的间距,由速度=路程÷时间可求出乙车的速度,结合甲、乙两车速度间的关系可求出甲车的速度,再求出乙车从A地返回时,两车的间距,依据相遇时间=5+两车间的间距÷两车速度和,即可求出甲、乙两车相遇的时间.
解:∵最终两车相距600千米,
∴A、C两地相距600千米.
乙车的速度为:(400+600)÷(11-1)=100(千米/小时),
乙车从B到达A地的时间为400÷100=4(小时),
甲车的速度为:(400-200)÷4=50(千米/小时),
乙车从A地返回时,两车的间距为:400-50×(4+1)=150(千米),
两车相遇的时间为:4+1+150÷(100+50)=4+1+1=6(小时);
故答案为:6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小美根据学习函数的经验,对函数y=
的图象与性质.小美根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究下面是小美的探究过程,请补充完整:
的图象与性质进行了探究下面是小美的探究过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | -2 | - | -1 | - |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | - | -1 | - |
|
|
| m |
|
| … |
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
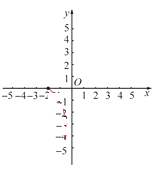
(4)结合函数的图象,写出该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民的交通消费可分为交通工具、交通工具使用燃料、交通工具维修、市内公共交通、城市间交通五项.该市统计局根据当年各项的权重及各项价格的涨幅,计算当年居民交通消费价格的平均涨幅.2017年该市的有关数据如下表所示.
交通工具 | 交通工具使用燃料 | 交通工具维修 | 市内公共交通 | 城市间交通 | |
占交通消费的比例 | 22% | 13% | 5% | P | 26% |
相对上一年价格的涨幅 | 1.5% | m% | 2% | 0.5% | 1% |
(1)求p的值;
(2)若2017年该市的居民交通消费相对上一年价格的平均涨幅为1.25%,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2020的直角顶点的坐标为_____.
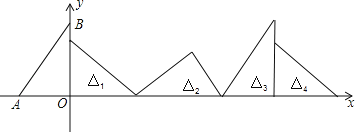
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠C=90°,BD平分∠ABC,过D作DE⊥BD交AB于点E,经过B,D,E三点作⊙O.
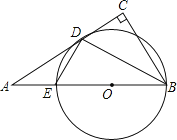
(1)求证:AC与⊙O相切于D点;
(2)若AD=15,AE=9,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据农业部提出“大力发展农村产业,实现乡村全面振兴”的方针,我市精确扶贫,指导某县大力发展大五星枇杷种植,去年、今年枇杷产量连续获得大丰收,该县枇杷销售采用线下销售和线上销售两种模式.
(1)今年该县种植专业户大五星枇杷产量为4500千克,全部售出,其中线上销售量不超过线下销售的4倍,求该种植专业户线下销售量至少多少千克?
(2)该种植专业户去年大五星枇杷线下销售均价为10元/千克,销售量为900千克,线上销售均价为8元/千克,销售量为1800千克,今年线下销售均价上涨![]() ,但销售量下降了
,但销售量下降了![]() ,线上销售均价上涨了
,线上销售均价上涨了![]() ,销量与去年持平,今年大五星枇杷的销售总额比去年销售总额减少了
,销量与去年持平,今年大五星枇杷的销售总额比去年销售总额减少了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-2(k-1)x+k2 =0有两个实数根x1.x2.
(1)求实 数k的取值范围;
(2)若(x1+1)(x2+1)=2,试求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面坐标系xOy中,点A的坐标为(1,0),点P的横坐标为2,将点A绕点P旋转,使它的对应点B恰好落在x轴上(不与A点重合);再将点B绕点O逆时针旋转90°得到点C.
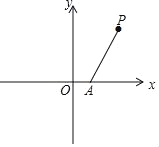
(1)直接写出点B和点C的坐标;
(2)求经过A,B,C三点的抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
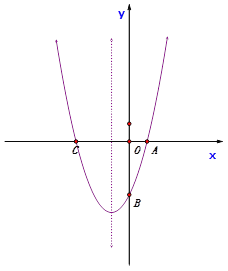
【题目】如图,已知抛物线![]() 经过点A(1,0)和点B (0,-3),与x轴交于另一点C。
经过点A(1,0)和点B (0,-3),与x轴交于另一点C。
(1)求抛物线的解析式。
(2)在抛物线上是否存在一点D,使△ACD的面积与△ABC的面积相等(点D不与点B重合)?若存在,求出点D的坐标;若不存在,请说明理由。
(3)若点P是抛物线上的动点,点Q是抛物线对称轴上的动点,那么是否存在这样的点P,使以点A、C、P、Q为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com