
【题目】如图,OP平分∠AOB,PA⊥OA、PB⊥OB,垂足分别为A、B,下列结论成立的是( )

①PA=PB;②PO平分∠APB;③OA=OB;④AB垂直平分OP
A.①③B.①②③C.②③D.①②③④
科目:初中数学 来源: 题型:
【题目】如图,AB是![]() 的直径,弦
的直径,弦![]() 于H,过CD延长线上一点E作
于H,过CD延长线上一点E作![]() 的切线交AB的延长线于
的切线交AB的延长线于![]() 切点为G,连接AG交CD于K.
切点为G,连接AG交CD于K.

![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,试判断AC与EF的位置关系,并说明理由;
,试判断AC与EF的位置关系,并说明理由;
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,
,![]() ,求FG的长.
,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
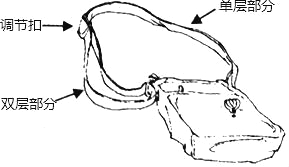
【题目】如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度y(cm) | … | 73 | 72 | 71 | … |
(1)根据表中数据的规律,完成以下表格,并直接写出y关于x的函数解析式;
(2)根据小敏的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为lcm,求l的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=40°,
(1)若点P是∠ABC与∠ACB平分线的交点,求∠P的度数;
(2)若点P是∠CBD与∠BCE平分线的交点,求∠P的度数;
(3)若点P是∠ABC与∠ACF平分线的交点,求∠P的度数;
(4)若∠A=β,求(1)(2)(3)中∠P的度数(用含β的代数式表示,直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为6 cm的等边三角形,动点P从A出发,以3 cm/s的速度,沿A-B-C向C运动,同时,动点Q从C出发沿CA方向以1 cm/s的速度向A运动,当其中一点运动到终点时,两点同时停止运动.设运动时间为t秒,当t= ____s,△APQ是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中,装有红球、白球、黄球共12个,这些球除颜色外完全相同,
从中随机摸出一个球,则:
(1)若盒子中有红球3个,则摸到红球的概率为_________;
(2)若摸到黄球的概率为![]() ,则该盒子中装有黄球的个数是__________个;
,则该盒子中装有黄球的个数是__________个;
(3)若将这12个球分别标上1至12这十二个数字,则摸到的数字是0的概率为________;摸到的数字是偶数的概率为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在街头巷尾会遇到一类“摸球游戏”,摊主把分别标有数字1,2,3的3个白球和标有数字4,5,6的3个黑球放在口袋里![]() 球除颜色外,其他均相同
球除颜色外,其他均相同![]() ,让你摸球
,让你摸球![]() 规定:每付3元钱就玩一局,每局连续摸两次,每次只能摸一个,第一次摸完后把球放回口袋里搅匀后再摸一次,若前后两次摸得的都是白球,摊主就送你10元钱的奖品.
规定:每付3元钱就玩一局,每局连续摸两次,每次只能摸一个,第一次摸完后把球放回口袋里搅匀后再摸一次,若前后两次摸得的都是白球,摊主就送你10元钱的奖品.
![]() 用列表法或树状图表示摸出的两个球可能出现的所有结果;
用列表法或树状图表示摸出的两个球可能出现的所有结果;
![]() 求获奖的概率.
求获奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com