【题目】在二次函数
，
与
的部分对应值如下表：
| … |
|
|
|
| … |
| … |
|
|
|
| … |
则下列说法：①图象经过原点；②图象开口向下；③图象经过点
；④当
时，随的增大而增大；⑤方程
有两个不相等的实数根．其中正确的是（ ）
A. ①②③ B. ①③⑤ C. ①③④ D. ①④⑤
【答案】B
【解析】
结合图表可以得出当x=0或2时，y=0，x=3时，y=3，根据此三点可求出二次函数解析式，从而得出抛物线的性质．
解：∵由图表可以得出当x=0或2时，y=0，x=3时，y=3，
∴
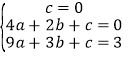
解得：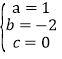
∴y=x2-2x，
∵c=0，∴图象经过原点，故①正确；
∵a=1＞0，
∴抛物线开口向上，故②错误；
把x=-1代入得，y=3，
∴图象经过点（-1，3），故③正确；
∵抛物线的对称轴是x=1，
∴x＞1时，y随x的增大而增大，x＜1时，y随x的增大而减小，故④错误；
∵抛物线y=ax2+bx+c与x轴有两个交点（0，0）、（2，0）
∴ax2+bx+c=0有两个不相等的实数根，故⑤正确；
故选：B．
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案科目：初中数学 来源： 题型：
【题目】王老师给学生出了一道题：求（2a+b）（2a﹣b）+2（2a﹣b）2+（2ab2﹣16a2b）÷（﹣2a）的值，其中a＝
，b＝﹣1，同学们看了题目后发表不同的看法．小张说：条件b＝﹣1是多余的．”小李说：“不给这个条件，就不能求出结果，所以不多余．”你认为他们谁说的有道理？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．求证：CE＝CF；
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD．
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE="10," 求直角梯形ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】探索题：(x﹣1)(x+1)＝x2﹣1；
(x﹣1)(x2+x+1)＝x3﹣1；
(x﹣1)(x3+x2+x+1)＝x4﹣1；
(x﹣1)(x4+x3+x2+x+1)＝x5﹣1
…
根据前面的规律，回答下列问题：
(1)(x﹣1)(xn+xn﹣1+xn﹣2+…+x3+x2+x+1)＝_____.
(2)当x＝3时，(3﹣1)(32015+32014+32013+…+33+32+3+1)＝______.
(3)求：22014+22013+22012+…+23+22+2+1的值.(请写出解题过程).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，△ABC内接于⊙O，AB为直径，∠CBA的平分线交AC于点F，交⊙O于点D，DE⊥AB于点E，且交AC于点P，连结AD．
（1）求证：∠DAC=∠DBA；
（2）求证：PD=PF；
（3）连接CD，若CD﹦3，BD﹦4，求⊙O的半径和DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在平面直角坐标系中，点
坐标为
，点
是
轴正半轴上一点，且
，点
是
轴上位于点右侧的一个动点，设点的坐标为
．
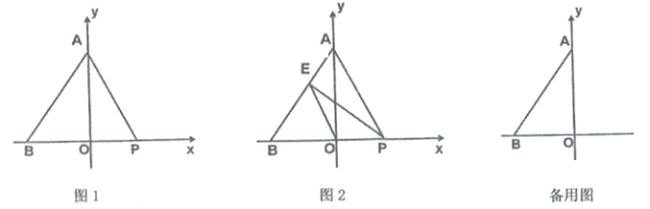
（1）点的坐标为（ ）；
（2）当
是等腰三角形时，求点的坐标；
（3）如图2，过点作
交线段
于点
，连接
，若点关于直线的对称点为
，当点恰好落在直线
上时，
．（直接写出答案）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在矩形ABCD中，动点E从A出发，沿AB→BC方向运动，当点E到达点C时停止运动，过点E做FE⊥AE，交CD于F点，设点E运动路程为x，FC=y，如图2所表示的是y与x的函数关系的大致图象，当点E在BC上运动时，FC的最大长度是
，则矩形ABCD的面积是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点D，E分别在AC，AB上，BD与CE相交于点O，已知∠B＝∠C，现添加下面的哪一个条件后，仍不能判定△ABD≌△ACE的是（ ）
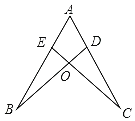
A.AD＝AEB.AB＝ACC.BD＝CED.∠ADB＝∠AEC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
