
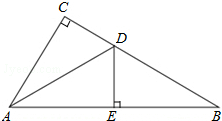
 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.分析 (1)由角平分线得出∠CAD=∠EAD,再由∠DEA=∠C和公共边,根据AAS证明△ACD≌△AED即可;
(2)由线段垂直平分线的性质得出AD=DB,由等腰三角形的性质得出∠B=∠EAD,因此∠CAD+∠EAD+∠B=90°,即可得出结果.
解答 (1)证明:∵AD平分∠CAB,
∴∠CAD=∠EAD,
∵DE⊥AB,
∴∠DEA=90°,
∴∠DEA=∠C,
在△ACD和△AED中,
$\left\{\begin{array}{l}{∠CAD=∠EAD}&{\;}\\{∠C=∠DEA}&{\;}\\{AD=AD}&{\;}\end{array}\right.$,
∴△ACD≌△AED(AAS).
(2)解:∵E为AB的中点,DE⊥AB,
∴AD=DB,
∴∠B=∠EAD,
∵∠CAD=∠EAD,
∴∠CAD=∠EAD=∠B,
∵∠CAD+∠EAD+∠B=90°,
∴∠B=30°.
点评 本题考查了全等三角形的判定与性质、线段垂直平分线的性质、角平分线的定义、等腰三角形的判定与性质;本题综合性强,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | y=(x-6)2+5 | B. | y=(x-3)2+5 | C. | y=(x-3)2-4 | D. | y=(x+3)2-9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由45°降为30°,已知原斜坡坡面AB长为200米,点D,B,C在同一水平地面上,求改善后的斜坡坡角向前推进的距离BD.(结果保留整数.参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由45°降为30°,已知原斜坡坡面AB长为200米,点D,B,C在同一水平地面上,求改善后的斜坡坡角向前推进的距离BD.(结果保留整数.参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 价格x (元/个) | … | 30 | 50 | … |
| 销售量y (万个) | … | 5 | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{6}$ | D. | $\frac{1}{3}$($\sqrt{3}$-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com