
【题目】如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为 . 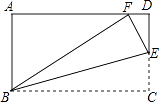
【答案】![]()
【解析】解:设CE=x. ∵四边形ABCD是矩形,
∴AD=BC=5,CD=AB=3,∠A=∠D=90°.
∵将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,
∴BF=BC=5,EF=CE=x,DE=CD﹣CE=3﹣x.
在Rt△ABF中,由勾股定理得:
AF2=52﹣32=16,
∴AF=4,DF=5﹣4=1.
在Rt△DEF中,由勾股定理得:
EF2=DE2+DF2 ,
即x2=(3﹣x)2+12 ,
解得:x= ![]() ,
,
故答案为 ![]() .
.
设CE=x,由矩形的性质得出AD=BC=5,CD=AB=3,∠A=∠D=90°.由折叠的性质得出BF=BC=5,EF=CE=x,DE=CD﹣CE=3﹣x.在Rt△ABF中利用勾股定理求出AF的长度,进而求出DF的长度;然后在Rt△DEF根据勾股定理列出关于x的方程即可解决问题.


科目:初中数学 来源: 题型:
【题目】如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4﹣x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.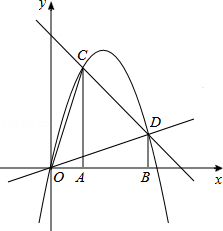
(1)求抛物线的表达式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中△AOC与△OBD重叠部分的面积记为S,试求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长都为 a 的正方形内分别排列着一些大小相等的圆:
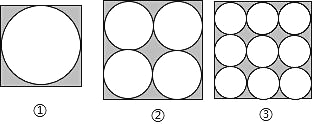
(1)根据图中的规律,第 4 个正方形内圆的个数是 ,第n 个正方形内圆的个数是_____.
(2)如果把正方形内除去圆的部分都涂上阴影.
①用含a 的代数式分别表示第 1 个正方形中、第 3 个正方形中阴影部分的面积(结果保留π);
②若 a=10,请直接写出第 2018 个正方形中阴影都分的面积 (结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠A和∠B互补,且∠A>∠B,给出下列四个式子:①90°﹣∠B;②∠A﹣90°;③![]() (∠A+∠B)④
(∠A+∠B)④![]() (∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
(∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
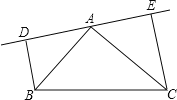
(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将举行“数学知识竞赛”活动,班长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:

请根据上面的信息,解决问题:
(1)试计算两种笔记本各买了多少本?
(2)请你解释:小明为什么不可能找回68元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,两名教师计划带领若干名学生去旅游,他们联系了报价均为每人500元的两家旅行社![]() 经协商,甲旅行社的优惠条件是:两名教师全额收费,学生都按七折收费;乙旅行社的优惠条件是:教师、学生都按八折收费
经协商,甲旅行社的优惠条件是:两名教师全额收费,学生都按七折收费;乙旅行社的优惠条件是:教师、学生都按八折收费![]() 请你帮他们选择一下,选哪家旅行社比较合算.
请你帮他们选择一下,选哪家旅行社比较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=120°,∠C=80°.将△BMN沿着MN翻折,得到△FMN.若MF∥AD,FN∥DC,则∠F的度数为( )
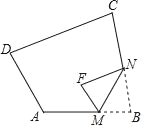
A. 70° B. 80° C. 90° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com