
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆,售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是20元.调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元,每减少1盆,盆景的平均每盆利润增加2元;
②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加![]() 盆,第二期盆景与花卉售完后的利润分别为
盆,第二期盆景与花卉售完后的利润分别为![]() ,
,![]() (单位:元)
(单位:元)
(1)用含![]() 的代数式分别表示
的代数式分别表示![]() ,
,![]() .
.
(2)当![]() 取何值时,第二期培植的盆录与花卉售完后获得的总利润
取何值时,第二期培植的盆录与花卉售完后获得的总利润![]() 最大,最大总利润是多少?
最大,最大总利润是多少?
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识
的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,
并将检查结果绘制成下面两个统计图.
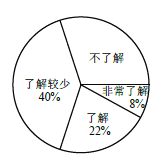
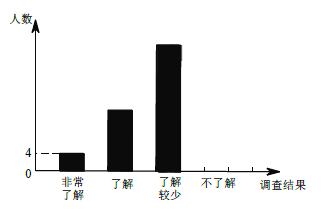
(1)本次调查的学生共有__________人,估计该校1200 名学生中“不了解”的人数是__________人.
(2)“非常了解”的4 人有![]() 两名男生,
两名男生,![]() 两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
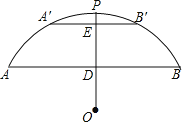
【题目】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
查看答案和解析>>
科目:初中数学 来源: 题型:
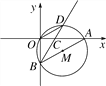
【题目】如图,在直角坐标系中,⊙M经过原点O(0,0),点A(![]() ,0)与点B(0,-
,0)与点B(0,-![]() ),点D在劣弧
),点D在劣弧![]() 上,连结BD交x轴于点C,且∠COD=∠CBO.
上,连结BD交x轴于点C,且∠COD=∠CBO.
(1)求⊙M的半径;
(2)求证:BD平分∠ABO;
(3)在线段BD的延长线上找一点E,使得直线AE恰为⊙M的切线,求此时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
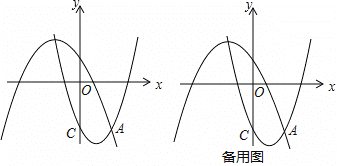
【题目】如图,在平面直角坐标系xOy中,抛物线L1:y=![]() +bx+c过点C(0,3),与抛物线L2:y=
+bx+c过点C(0,3),与抛物线L2:y=![]()
![]() x+2的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、L2上的动点。
x+2的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、L2上的动点。
(1)求抛物线L1对应的函数表达式;
(2)若以点A. C.P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
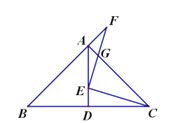
【题目】在△ABC中,AB=AC,∠BAC=90°,AD是△ABC斜边BC上的高,E是AD上一点,连接EC,过点E作EF⊥EC交射线BA于点F.AC、EF交于点G,△ECG与△AFG的面积差为1,则线段AE=___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动画片《小猪佩奇》分靡全球,受到孩子们的喜爱.现有4张《小猪佩奇》角色卡片,分别是A佩奇,B乔治,C佩奇妈妈,D佩奇爸爸(四张卡片除字母和内容外,其余完全相同).姐弟两人做游戏,他们将这四张卡片混在一起,背面朝上放好.
(1)姐姐从中随机抽取一张卡片,恰好抽到A佩奇的概率为 ;
(2)若两人分别随机抽取一张卡片(不放回),请用列表或画树状图的分方法求出恰好姐姐抽到A佩奇弟弟抽到B乔治的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com