
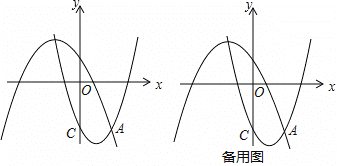
【题目】如图,在平面直角坐标系xOy中,抛物线L1:y=![]() +bx+c过点C(0,3),与抛物线L2:y=
+bx+c过点C(0,3),与抛物线L2:y=![]()
![]() x+2的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、L2上的动点。
x+2的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、L2上的动点。
(1)求抛物线L1对应的函数表达式;
(2)若以点A. C.P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;
【答案】(1)抛物线L1:y=![]() -2x-3;(2)点P的坐标为(-1,0),(3,0)或(-
-2x-3;(2)点P的坐标为(-1,0),(3,0)或(-![]() );
);
【解析】
(1)先求出A点的坐标,再用待定系数法求出函数解析式便可;
(2)设点P的坐标为(x,x2-2x-3),分两种情况讨论:AC为平行四边形的一条边,AC为平行四边形的一条对角线,用x表示出Q点坐标,再把Q点坐标代入抛物线L2:y=![]()
![]() x+2中,列出方程求得解便可.
x+2中,列出方程求得解便可.
(1) 将x=2代入y=![]()
![]() x+2,得y=3,
x+2,得y=3,
故点A的坐标为(2,-3),
将A(2,-1), C(0,3)代入y=![]() +bx+c,
+bx+c,
得-3=![]() +2b+c ,-3=0+0+c,
+2b+c ,-3=0+0+c,
解得b=-2,c=-3,
∴抛物线L1:y=![]() -2x-3;
-2x-3;
(2)设点P的坐标为(x,![]() -2x-3),
-2x-3),
第一种情况:AC为平行四边形的一条边,
①当点Q在点P右侧时,则点Q的坐标为(x+2,![]() -2x-3),
-2x-3),
将Q(x+2,![]() -2x-3)代入y=
-2x-3)代入y=![]()
![]() x+2得,
x+2得,![]() -2x-3=
-2x-3=![]() -
-![]() +2,
+2,
解得,x=0或x=-1,
因为x=0时,点P与C重合,不符合题意,所以舍去,
此时点P的坐标为(-1,0);
②当点Q在点P左侧时,则点Q的坐标为(x-2,![]() -2x-3),
-2x-3),
将Q(x-2,![]() -2x-3)代入y=
-2x-3)代入y=![]()
![]() x+2得,
x+2得,![]() -2x-3=
-2x-3=![]() -
-![]() +2,
+2,
解得,x=3,或x=-![]() ,此时P点的坐标为(3,0)或(-
,此时P点的坐标为(3,0)或(-![]() );
);
第二种情况:当AC为平行四边形的一条对角线时,
由AC的中点坐标为(1,-3),得PQ的中点坐标为(1,-3),
故点Q的坐标为(2-x,-![]() +2x-3),
+2x-3),
将Q(2-x,-![]() +2x-3)代入y=
+2x-3)代入y=![]()
![]() x+2得,-
x+2得,-![]() +2x-3=
+2x-3=![]() -
-![]() +2,
+2,
解得,x=0或x=-3,
因为x=0时,点P与点C重合,不符合题意,所以舍去,
此时点P的坐标为(-3,12),
综上所述,点P的坐标为(-1,0),(3,0)或(-![]() )或(-3,12).
)或(-3,12).


科目:初中数学 来源: 题型:
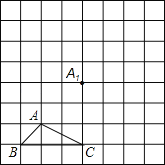
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RtΔABC中,∠C=90°,AC=4,BC=3.

(1)如图(1),四边形DEFG为ABC的内接正方形,求正方形的边长.
(2)如图(2),三角形内有并排的两个相等的正方形,它们组成的矩形内接于ΔABC,求正方形的边长.
(3)如图(3),三角形内有并排的三个相等的正方形,它们组成的矩形内接于ΔABC,求正方形的边长.
(4) 如图(4),三角形内有并排的n个相等的正方形,它们组成的矩形内接于ΔABC,请写出正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆,售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是20元.调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元,每减少1盆,盆景的平均每盆利润增加2元;
②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加![]() 盆,第二期盆景与花卉售完后的利润分别为
盆,第二期盆景与花卉售完后的利润分别为![]() ,
,![]() (单位:元)
(单位:元)
(1)用含![]() 的代数式分别表示
的代数式分别表示![]() ,
,![]() .
.
(2)当![]() 取何值时,第二期培植的盆录与花卉售完后获得的总利润
取何值时,第二期培植的盆录与花卉售完后获得的总利润![]() 最大,最大总利润是多少?
最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
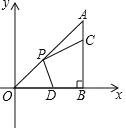
【题目】如图,在Rt△ABO中,∠OBA=90°,A(4,4),点C在边AB上,且![]() ,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为_______.
,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
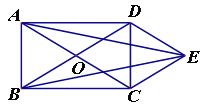
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为菱形;
(2)连接AE、BE,AE与BE相等吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中错误的命题有( )
①线段垂直平分线上的点与这条线段两端点距离相等;
②若两三角形关于直线L对称,则对应线段所在的直线必相交,且交点在对称轴上;
③顶角和底边对应相等的两个等腰三角形全等;
④一腰和一腰上的高对应相等的两个等腰三角形全等;
⑤有一边上的高也是这边上的中线的等腰三角形是等边三角形
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为评估九年级学生的学习成绩状况,以应对即将到来的中考做好教学调整,某中学抽取了部分参加考试的学生的成绩作为样本分析,绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
(1)求本中学成绩类别为“中”的人数;
(2)求出扇形图中,“优”所占的百分比,并将条形统计图补充完整;
(3)该校九年级共有1000人参加了这次考试,请估算该校九年级共有多少名学生的数学成绩达到优秀?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com