【题目】下列命题中错误的命题有( )
①线段垂直平分线上的点与这条线段两端点距离相等；
②若两三角形关于直线L对称，则对应线段所在的直线必相交，且交点在对称轴上；
③顶角和底边对应相等的两个等腰三角形全等；
④一腰和一腰上的高对应相等的两个等腰三角形全等；
⑤有一边上的高也是这边上的中线的等腰三角形是等边三角形
A.1个B.2个C.3个D.4个
【答案】B
【解析】
①根据垂直平分线的性质判断命题的真假；
②根据两个图形成轴对称的知识判断命题的真假；
③④根据证明三角形全等的方法判断命题的真假；
⑤根据等边三角形的证明方法判断命题的真假．
解：线段垂直平分线上的点到线段的两个端点的距离相等，所以命题①是真命题；
若两三角形关于直线L对称，则对应线段所在的直线相交或平行，若对应线段所在的直线相交，且交点在对称轴上，所以命题②是假命题；
顶角相等的两个等腰三角形，三个角都相等，且底边对应相等，则根据ASA或AAS可证这两个等腰三角形全等，所以命题③是真命题；
这两个等腰三角形可分为钝角三角形和锐角三角形来讨论，如下图的甲乙两个等腰三角形：
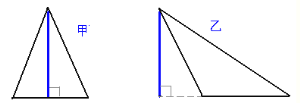
则可知这两个三角形不全等，所以命题④是假命题；
任意等腰三角形底边上的高线也是中线，因此有一边上的高也是这边上的中线的等腰三角形不一定是等边三角形，所以命题⑤是假命题．
故答案选：B．
科目：初中数学 来源： 题型：
【题目】如图①，在△AOB 中，∠AOB＝90，OA＝3，OB＝4．将△AOB 沿 x 轴依次以点 A、B、O为旋转中心顺时针旋转，分别得到图②图③、…，则旋转得到的图⑧的直角顶点的坐标为____.
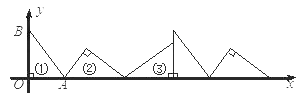
查看答案和解析>>
科目：初中数学 来源： 题型：
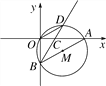
【题目】如图，在直角坐标系中，⊙M经过原点O(0，0)，点A(
，0)与点B(0，－
)，点D在劣弧
上，连结BD交x轴于点C，且∠COD＝∠CBO.
(1)求⊙M的半径；
(2)求证：BD平分∠ABO；
(3)在线段BD的延长线上找一点E，使得直线AE恰为⊙M的切线，求此时点E的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
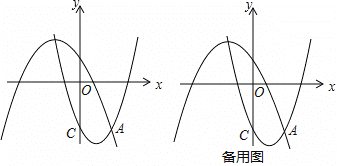
【题目】如图,在平面直角坐标系xOy中,抛物线L1:y=
+bx+c过点C(0,3),与抛物线L2:y=
x+2的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、L2上的动点。
(1)求抛物线L1对应的函数表达式；
(2)若以点A. C.P、Q为顶点的四边形恰为平行四边形，求出点P的坐标；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某学校计划利用一片空地建一个学生自行车车棚，自行车车棚为矩形，其中一面靠墙，这堵墙的长度为
，另三面墙用现有的木板材料围成，总长为
，且计划建造车棚的面积为
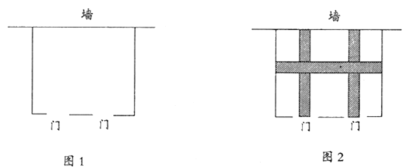
（1）如图1，为了方便学生出行，学校决定在与墙平行的一面留两个
宽的门，求这个车棚的长和宽；
（2）如图2，为了方使学生停取车，施工单位又决定在车棚内修建一条平行于墙和两条垂直于墙的
条等宽小路，使得剩余面积为
，求小路的宽度。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB=AC，∠BAC=90°，AD是△ABC斜边BC上的高，E是AD上一点，连接EC，过点E作EF⊥EC交射线BA于点F.AC、EF交于点G，△ECG与△AFG的面积差为1，则线段AE=___.
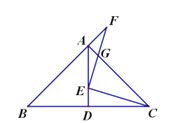
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在水果销售旺季，某水果店购进一优质水果，进价为20元/千克，售价不低于20元/千克，且不超过32元/千克，根据销售情况，发现该水果一天的销售量y（千克）与该天的售价x（元/千克）满足如下表所示的一次函数关系．
销售量y（千克） | … | 34.8 | 32 | 29.6 | 28 | … |
售价x（元/千克） | … | 22.6 | 24 | 25.2 | 26 | … |
（1）某天这种水果的售价为23.5元/千克，求当天该水果的销售量．
（2）如果某天销售这种水果获利150元，那么该天水果的售价为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，甲船以每小时30
海里的速度向正北方向航行，当甲船位于A1处时，乙船位于甲船的北偏西105°方向的B1处，且乙船从B1处按北偏东15°方向匀速直线航行，当甲船航行20分钟到达A2时，乙船航行到甲船的北偏西120°方向的B2处，此时两船相距10海里．
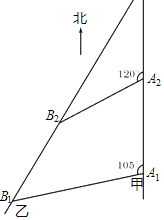
（1）判断△A1A2B2的形状，并给出证明；
（2）求乙船每小时航行多少海里？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：
我们知道，四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形相似（不全等），我们就把这条对角线叫做这个四边形的“相似对角线”．
理解：
（1）如图1，已知Rt△ABC在正方形网格中，请你只用无刻度的直尺在网格中找到一点D，使四边形ABCD是以AC为“相似对角线”的四边形（保留画图痕迹，找出3个即可）；
（2）如图2，在四边形ABCD中，∠ABC=80°，∠ADC=140°，对角线BD平分∠ABC．
求证：BD是四边形ABCD的“相似对角线”；
（3）如图3，已知FH是四边形EFCH的“相似对角线”，∠EFH=∠HFG=30°，连接EG，若△EFG的面积为2
，求FH的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com