
����Ŀ����ͼ���״���ÿСʱ30![]() ������ٶ������������У����״�λ��A1��ʱ���Ҵ�λ�ڼ״��ı�ƫ��105�������B1�������Ҵ���B1������ƫ��15����������ֱ�ߺ��У����״�����20���ӵ���A2ʱ���Ҵ����е��״��ı�ƫ��120�������B2������ʱ�������10
������ٶ������������У����״�λ��A1��ʱ���Ҵ�λ�ڼ״��ı�ƫ��105�������B1�������Ҵ���B1������ƫ��15����������ֱ�ߺ��У����״�����20���ӵ���A2ʱ���Ҵ����е��״��ı�ƫ��120�������B2������ʱ�������10![]() ���
���
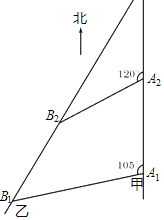
��1���жϡ�A1A2B2����״��������֤����
��2�����Ҵ�ÿСʱ���ж��ٺ��
���𰸡���1����A1A2B2�ǵȱ������Σ���2��20![]() ����
����
��������
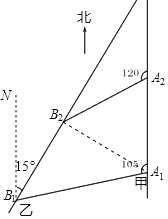
��1���ɸ����ĽǶȼ������θ��߳����ó���A1A2B2����״.
��2�������B1B2�ľ���������ʱ������Ҵ����е��ٶ�.
��1����A1A2B2�ǵȱ������Σ��������£�
����A1B2��
�״���ÿСʱ30![]() ������ٶ������������У�����20���ӵ���A2��
������ٶ������������У�����20���ӵ���A2��
��A1A2��30![]() ��10
��10![]() ��
��
�֡�A2B2��10![]() ����A1A2B2��60����
����A1A2B2��60����
���A1A2B2�ǵȱ������Σ�
��2������B��B1N��A1A2����ͼ��
��B1N��A1A2��
���A1B1N��180������B1A1A2��180����105����75����
���A1B1B2��75����15����60����
�ߡ�A1A2B2�ǵȱ������Σ�
���A2A1B2��60����A1B2��A1A2��10![]() ��
��
���B1A1B2��105����60����45����
�ڡ�B1A1B2�У�
��A1B2��10![]() ����B1A1B2��45������A1B1B2��60����
����B1A1B2��45������A1B1B2��60����
����B��BE��A1B1,
�����Ҷ��������B1B2�� ��
��
�����Ҵ�ÿСʱ���У�![]() ���
���


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90����AC=4��BC=3.

��1����ͼ��1�����ı���DEFGΪABC���ڽ������Σ��������εı߳�.
��2����ͼ��2�������������в��ŵ�������ȵ������Σ�������ɵľ����ڽ�����ABC���������εı߳�.
��3����ͼ��3�������������в��ŵ�������ȵ������Σ�������ɵľ����ڽ�����ABC���������εı߳�.
��4�� ��ͼ��4�������������в��ŵ�n����ȵ������Σ�������ɵľ����ڽ�����ABC����д�������εı߳�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������д����������( )
���߶δ�ֱƽ�����ϵĵ��������߶����˵������ȣ�
�����������ι���ֱ��L�Գƣ����Ӧ�߶����ڵ�ֱ�߱��ཻ���ҽ����ڶԳ����ϣ�
�����Ǻ͵ױ߶�Ӧ��ȵ���������������ȫ�ȣ�
��һ����һ���ϵĸ߶�Ӧ��ȵ���������������ȫ�ȣ�
����һ���ϵĸ�Ҳ������ϵ����ߵĵ����������ǵȱ�������
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������꼶ѧ����ѧϰ�ɼ�״������Ӧ�Լ����������п����ý�ѧ������ij��ѧ��ȡ�˲��ֲμӿ��Ե�ѧ���ijɼ���Ϊ�������������Ƴ�������������������ͳ��ͼ�������ͼ���ṩ����Ϣ����������⣺
��1������ѧ�ɼ����Ϊ���С���������
��2���������ͼ�У����š���ռ�İٷֱȣ���������ͳ��ͼ����������
��3����У���꼶����1000�˲μ�����ο��ԣ�������У���꼶���ж�����ѧ������ѧ�ɼ��ﵽ���㣿

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c��x���ཻ��A.B���㣬��A�ڵ�B��࣬����������M��P��N���ƶ������ǵ�����ֱ�ΪM����1��4��.P��3��4��.N��3��1���������������ƶ������У���A���������СֵΪ��3����a��b+c����Сֵ�ǣ�������
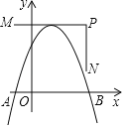
A.��15B.��12C.��4D.��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+(2m+1)x+m2��1��0����������ȵ�ʵ����.
����m��ȡֵ��Χ;
����x1,x2�Ƿ��̵�������x12+x22+x1x2��17��0,��m��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
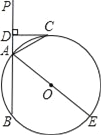
����Ŀ����ͼ����ֱ֪��PA����O��A��B���㣬AE����O��ֱ������CΪ��O��һ�㣬��ACƽ����PAE����C��CD��PA������ΪD��
��1����֤��CDΪ��O�����ߣ�
��2����DC+DA=6����O��ֱ��Ϊ10����AB�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() ��һ�κ���
��һ�κ���![]() ��ͼ��ͷ���������
��ͼ��ͷ���������![]() ��ͼ����������㣮
��ͼ����������㣮
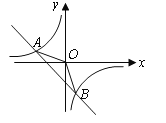
��1������������һ�κ����Ľ���ʽ��
��2������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̼�����ɫ���С������г�����Ϊ����ϲ���Ľ�ͨ���ߣ�ij�˶��̳ǵ����г���������2015�����������ӣ���ͳ�ƣ����̳�1�·��������г�64����3�·�������100����
��1�������̳�ǰ4���µ����г���������ƽ����������ͬ���ʸ��̳�4�·��������������г���
��2�����ǵ����г��������ӣ����̳���Ͷ��3��Ԫ�ٹ���һ�����ֹ������г�����֪![]() �ͳ��Ľ���Ϊ500Ԫ/�����ۼ�Ϊ700Ԫ/����
�ͳ��Ľ���Ϊ500Ԫ/�����ۼ�Ϊ700Ԫ/����![]() �ͳ�����Ϊ1000Ԫ/�����ۼ�Ϊ1300Ԫ/�����������۾��飬
�ͳ�����Ϊ1000Ԫ/�����ۼ�Ϊ1300Ԫ/�����������۾��飬![]() �ͳ�������������
�ͳ�������������![]() �ͳ���2������������
�ͳ���2������������![]() �ͳ���2.8����������������ȫ�����꣬Ϊʹ��������̳�Ӧ��ν�����
�ͳ���2.8����������������ȫ�����꣬Ϊʹ��������̳�Ӧ��ν�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com