
【题目】“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2015年起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆.
(1)若该商城前4个月的自行车销量的月平均增长率相同,问该商城4月份卖出多少辆自行车.
(2)考虑到自行车需求不断增加,该商城准备投入3万元再购进一批两种规格的自行车,已知![]() 型车的进价为500元/辆,售价为700元/辆,
型车的进价为500元/辆,售价为700元/辆,![]() 型车进价为1000元/辆,售价为1300元/辆.根据销售经验,
型车进价为1000元/辆,售价为1300元/辆.根据销售经验,![]() 型车进货量不少于
型车进货量不少于![]() 型车的2倍,但不超过
型车的2倍,但不超过![]() 型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?
型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?
【答案】(1)该商城4月份卖出125辆自行车;(2)该商城应购进![]() 型车34辆,
型车34辆,![]() 型车13辆.
型车13辆.
【解析】
(1)设前4个月自行车销量的月平均增长率为a,根据题意列出一元二次方程即可求解;
(2)设进![]() 型车
型车![]() 辆,则进
辆,则进![]() 型车
型车![]() 辆,根据题意得到不等式组求出x的取值,再根据利润的定义得到利润的一次函数,根据一次函数的增减性即可求解.
辆,根据题意得到不等式组求出x的取值,再根据利润的定义得到利润的一次函数,根据一次函数的增减性即可求解.
解:(1)设前4个月自行车销量的月平均增长率为a,
根据题意列方程:![]() ,
,
解得![]() (不合题意,舍去),
(不合题意,舍去),![]() .
.
![]() (辆).
(辆).
答:该商城4月份卖出125辆自行车.
(2)设进![]() 型车
型车![]() 辆,则进
辆,则进![]() 型车
型车![]() 辆,
辆,
根据题意得不等式组
![]() ,
,
解得![]() ,自行车辆数为整数,所以
,自行车辆数为整数,所以![]() .
.
销售利润![]() .
.
整理得![]() ,
,
∵![]() 随着
随着![]() 的增大而减小,
的增大而减小,
∴当![]() 时,销售利润
时,销售利润![]() 的最大值.
的最大值.
此时,![]() .
.
所以该商城应购进![]() 型车34辆,
型车34辆,![]() 型车13辆.
型车13辆.


科目:初中数学 来源: 题型:
【题目】如图,甲船以每小时30![]() 海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10![]() 海里.
海里.
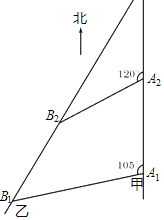
(1)判断△A1A2B2的形状,并给出证明;
(2)求乙船每小时航行多少海里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,F是⊙O上一点,连接FO、FB.C为![]() 中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.
中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.
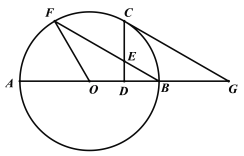
(1)求证:CG是⊙O的切线;
(2)若![]() BOF=120°,且CE=4,求⊙O的半径.
BOF=120°,且CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com