
【题目】如图,AB是⊙O的直径,F是⊙O上一点,连接FO、FB.C为![]() 中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.
中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.
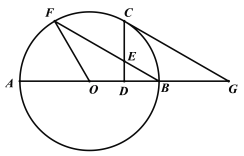
(1)求证:CG是⊙O的切线;
(2)若![]() BOF=120°,且CE=4,求⊙O的半径.
BOF=120°,且CE=4,求⊙O的半径.
【答案】(1)见解析;(2)⊙O的半径为4![]()
【解析】
(1)连接OC,利用垂径定理得到OC⊥BF,根据CG∥FB得到∠OCG=90°即可求解;
(2)连接BC,由(1)知,∠COB =60°,得到△OBC为等边三角形.,由CD⊥OB得到∠OCD=30°,求出EM=![]() CE=2,利用勾股定理求出CM=
CE=2,利用勾股定理求出CM=![]() ,再根据等腰三角形“三线合一”得OM=CM=
,再根据等腰三角形“三线合一”得OM=CM=![]() ,故OC=4
,故OC=4![]() ,即为半径长.
,即为半径长.
(1)证明:连接OC.
∵点C为![]() 的中点,
的中点,
∴![]() ,
,
所以∠COB=∠COF,
因为OB=OF,
所以OC⊥BF,
设垂足为M,则∠OMB=90°.
因为CG∥FB,
所以∠OCG=∠OMB=90°,
所以CG是⊙O的切线.
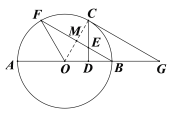
(2)解:连接BC.
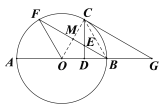
由(1)知,∠COB=∠COF=![]() ∠BOF=60°,
∠BOF=60°,
因为OB=OC,
所以△OBC为等边三角形,∠OCB=60°,
∵CD⊥OB,
∴CD平分∠OCB,
∴∠OCD=30°,
则EM=![]() CE=2,
CE=2,
又OC⊥BF,
所以CM=![]() .
.
∴OM=CM=![]() ,
,
所以OC=4![]() ,即⊙O的半径为4
,即⊙O的半径为4![]()


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:
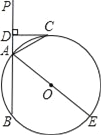
【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.将抛物线沿y轴平移t(t>0)个单位,当平移后的抛物线与线段OB有且只有一个交点时,则t的取值范围是___.
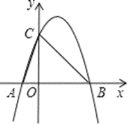
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2015年起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆.
(1)若该商城前4个月的自行车销量的月平均增长率相同,问该商城4月份卖出多少辆自行车.
(2)考虑到自行车需求不断增加,该商城准备投入3万元再购进一批两种规格的自行车,已知![]() 型车的进价为500元/辆,售价为700元/辆,
型车的进价为500元/辆,售价为700元/辆,![]() 型车进价为1000元/辆,售价为1300元/辆.根据销售经验,
型车进价为1000元/辆,售价为1300元/辆.根据销售经验,![]() 型车进货量不少于
型车进货量不少于![]() 型车的2倍,但不超过
型车的2倍,但不超过![]() 型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?
型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标为x1、x2,其中﹣2<x1<﹣1、0<x2<1下列结论:①4a﹣2b+c<0②2a﹣b<0③abc>0④b2+8a>4ac正确的结论是_____.
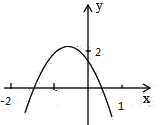
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于点F.
(1)若⊙O的半径为3,∠CDF=15°,求阴影部分的面积;
(2)求证:DF是⊙O的切线;
(3)求证:∠EDF=∠DAC.
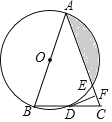
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC 中,D是边AC上一点,连接BD,将ΔBCD绕点B逆时针旋转60°,得到ΔBAE,连接ED.若BC=5,BD=4.5,则下列结论错误的是( )
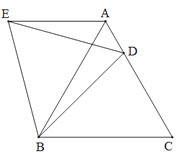
A.AE∥BCB.∠ADE=∠BDC
C.ΔBDE是等边三角形D.ΔADE的周长是9.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com