
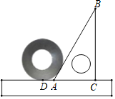
【题目】把直尺、三角尺和圆形螺母按如图所示放置于桌面上,∠CAB=60°,若量出AD=6cm,则圆形螺母的外直径是___.
科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,F是⊙O上一点,连接FO、FB.C为![]() 中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.
中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.
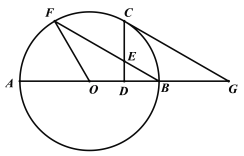
(1)求证:CG是⊙O的切线;
(2)若![]() BOF=120°,且CE=4,求⊙O的半径.
BOF=120°,且CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小阳,小杰和小凡到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为10元/千克,下面是他们在活动结束后的对话.
小阳:如果以12元/千克的价格销售,那么每天可售出300千克.
小杰:如果以15元/千克的价格销售,那么每天可获取利润750元.
小凡:我通过调查验证发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系.
(1)求y(千克)与x(元)(x>0)的函数关系式;
(2)当销售单价为何值时,该超市销售这种水果每天获得的利润达600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是二次函数![]() 图象的一部分,图象过点
图象的一部分,图象过点![]() ,二次函数图象对称轴为直线
,二次函数图象对称轴为直线![]() ,给出五个结论:①
,给出五个结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 的增大而增大;④方程
的增大而增大;④方程![]() 的根为
的根为![]() ,
,![]() ,;⑤
,;⑤![]() 其中正确结论是( )
其中正确结论是( )
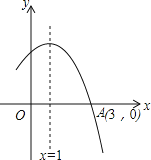
A.①③④B.①②③C.②③④D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
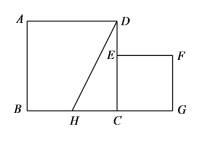
【题目】如图,已知正方形ABCD的边长为1,正方形CEFG的面积为![]() ,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为
,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为![]() ,且
,且![]() .
.
⑴求线段CE的长;
⑵若点H为BC边的中点,连结HD,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com