
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴的负半轴交于点
轴的负半轴交于点![]() 、与
、与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)如果点![]() 是抛物线上一点,联结
是抛物线上一点,联结![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,
,![]() ,求
,求![]() 的坐标.
的坐标.
【答案】(1)1 (2)(4,12)
【解析】
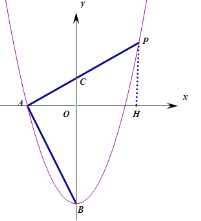
(1)先根据y轴上点的坐标特征确定B(0,-4),再利用勾股定理计算出OA=2,则A点坐标为(-2,0),然后把A点坐标代入y=ax2-4求出a的值即可得到抛物线解析式;
(2)作PH⊥x轴于点H,则AH=x+3,PH∥BC,根据平行线分线段成比例定理求出点P的横坐标,进而可求出点P的坐标.
(1)当x=0时,y=ax2-4=-4,则B(0,-4),所以OB=4,
在Rt△OAB中,OA= ![]() =2,
=2,
∴A点坐标为(-2,0),
把A(-2,0)代入y=ax2-4得4a-4=0,
解得a=1;
(2∵a=1,
∴抛物线解析式为y=x2-4.
设P(x,x2-4).
∵![]() ,
,
∴![]() ,
,
作PH⊥x轴于点H,则AH=x+3,PH∥BC,
∴![]() ,
,
∴![]() ,
,
∴x=4,
∴y= x2-4=12,
∴P(4,12).


科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2015年起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆.
(1)若该商城前4个月的自行车销量的月平均增长率相同,问该商城4月份卖出多少辆自行车.
(2)考虑到自行车需求不断增加,该商城准备投入3万元再购进一批两种规格的自行车,已知![]() 型车的进价为500元/辆,售价为700元/辆,
型车的进价为500元/辆,售价为700元/辆,![]() 型车进价为1000元/辆,售价为1300元/辆.根据销售经验,
型车进价为1000元/辆,售价为1300元/辆.根据销售经验,![]() 型车进货量不少于
型车进货量不少于![]() 型车的2倍,但不超过
型车的2倍,但不超过![]() 型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?
型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电商平台长期销售A型商品,2017年以4800元购进该型号商品并且全部售完;2019年,这种型号的商品的进价比2017年下降了9元/件,该平台用3000元购进了与2017年相同数量的该A型商品也全部售完,这两年A型商品的售价均为40元/件.
(1)2017年A型商品的进价是多少元/件?
(2)若该电商平台每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题时,我们常常从特殊入手,猜想结论,并尝试发现解决问题的策略与方法.
(问题提出)
求证:如果一个定圆的内接四边形对角线互相垂直,那么这个四边形的对边的平方和是一个定值.
(从特殊入手)
我们不妨设定圆O的半径是R,⊙O的内接四边形ABCD中,AC⊥BD.
请你在图①中补全特殊殊位置时的图形,并借助于所画图形探究问题的结论.

(问题解决)
已知:如图②,定圆⊙O的半径是R,四边形ABCD是⊙O的内接四边形, AC⊥BD.
求证: .
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
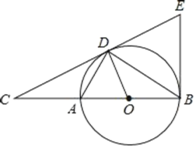
(1)判断直线CD和⊙O的位置关系,并说明理由;
(2)过点B作⊙O的切线BE交直线CD于点E,若BE=5,CD=8,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“童舒”童装商场某种童装进价为每件60元,当售价为每件100元时,每天可卖出120件:童装的售价每上涨1元,则每天少卖2件.为了让利于顾客,商场规定销售这种重装时利润率不能超过90%,则当每件童装的售价定为多少元时,商场销售此种童装时每天可获得最大利润?每天的最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com