
【题目】如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
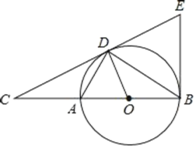
(1)判断直线CD和⊙O的位置关系,并说明理由;
(2)过点B作⊙O的切线BE交直线CD于点E,若BE=5,CD=8,求⊙O的半径.
【答案】(1)直线CD和⊙O的位置关系是相切,理由见解析;(2)⊙O的半径为![]() .
.
【解析】
(1)因为直径所对的圆周角是90°,所以∠ADB=90°,所以∠DAB+∠DBA=90°,
又因为OD=OA,所以得出∠DAB=∠ADO,之后进一步求解即可。
(2)根据CD是⊙O的切线,BE是⊙O的切线,所以得出DE=BE=5,∠CBE=90°=∠CDO,再利用勾股定理求出BC的长,进一步证明△COD∽△CEB,之后利用相似三角形性质求解即可。
(1)直线CD和⊙O的位置关系是相切,理由如下:
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠DBA=90°,
∵∠CDA=∠CBD,
∴∠DAB+∠CDA=90°,
∵OD=OA,
∴∠DAB=∠ADO,
∴∠CDA+∠ADO=90°,
即∠CDO=90°,
∴OD⊥CE,
∴直线CD是⊙O的切线;
(2)∵CD是⊙O的切线,BE是⊙O的切线,
∴DE=BE=5,∠CBE=90°=∠CDO,
∴CE=CD+DE=13,
∴BC=![]() =
=![]() ,
,
∵∠C=∠C,∴△COD∽△CEB,
∴![]() =
=![]() ,即
,即![]() ,
,
解得:OC=![]() ,
,
∴OB=BC﹣OC=![]() ,
,
即⊙O的半径为![]() .
.


科目:初中数学 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA
与⊙O的另一个交点为E,连结AC,CE。

(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
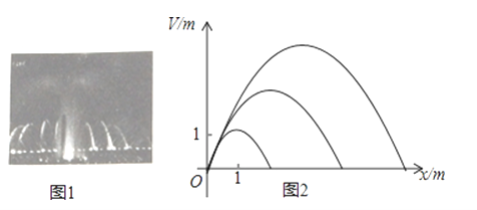
【题目】音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a、b的值;
(2)若k=1,喷出的水恰好达到岸边,则此时喷出的抛物线水线最大高度是多少米?
(3)若k=3,a=﹣![]() ,则喷出的抛物线水线能否达到岸边?
,则喷出的抛物线水线能否达到岸边?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图.
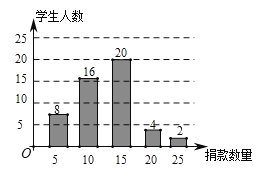
(1)这50名同学捐款的众数为 元,中位数为 元;
(2)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
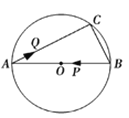
【题目】如图,AB是⊙O的直径,弦BC=6cm,AC=8cm.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q以1cm/s的速度从A点出发沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
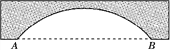
【题目】如图,一拱形公路桥,圆弧形桥拱的水面跨度AB=80 m,桥拱到水面的最大高度为20 m.(1)求桥拱的半径.
(2)现有一艘宽60 m,顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com