
分析 首先利用将原式变形为$\sqrt{(x-\frac{1}{x})^{2}}$,然后在确定出x$-\frac{1}{x}$的正负,最后再根据$\sqrt{{a}^{2}}=|a|$进行化简即可.
解答 解:原式=$\sqrt{(x-\frac{1}{x})^{2}}$,
当0<x<1时,x-$\frac{1}{x}$<0,
原式=$\sqrt{(x-\frac{1}{x})^{2}}$=|x$-\frac{1}{x}$|=$\frac{1}{x}-x$;
当-1<x<0时,x-$\frac{1}{x}$>0,
原式=x-$\frac{1}{x}$;
当x≤-1时,x-$\frac{1}{x}$≤0,
原式=$\frac{1}{x}-x$.
综上所述,当0<x<1或x≤-1时,$\sqrt{{x}^{2}-2+\frac{1}{{x}^{2}}}$=$\frac{1}{x}-x$;当-1<x<0时,$\sqrt{{x}^{2}-2+\frac{1}{{x}^{2}}}$=x-$\frac{1}{x}$;
点评 本题主要考查的是二次根式的化简,解答本题需要同学们掌握公式:$\sqrt{{a}^{2}}=|a|$,求得x-$\frac{1}{x}$的正负是解题的关键.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:选择题
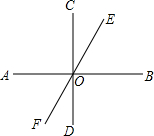 如图所示,直线AB,CD,EF相交于点O,且AB⊥CD于点O,∠BOE=70°,则∠FOD等于( )
如图所示,直线AB,CD,EF相交于点O,且AB⊥CD于点O,∠BOE=70°,则∠FOD等于( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
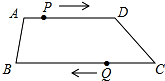 如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.
如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com